
Question Number 130921 by pticantor last updated on 30/Jan/21
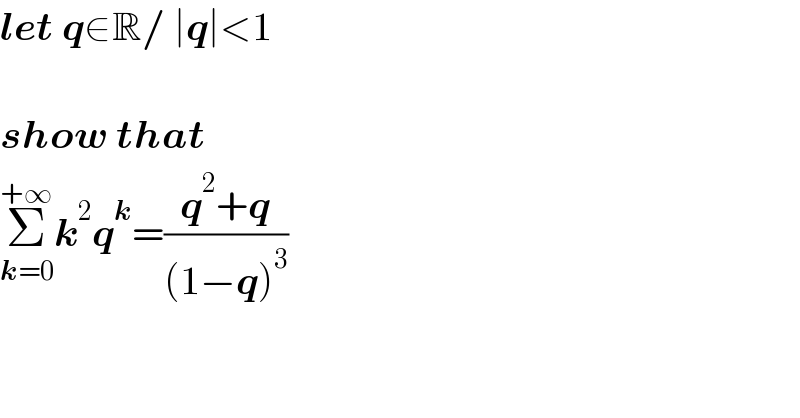
$$\boldsymbol{{let}}\:\boldsymbol{{q}}\in\mathbb{R}/\:\mid\boldsymbol{{q}}\mid<\mathrm{1} \\ $$ $$\: \\ $$ $$\boldsymbol{{show}}\:\boldsymbol{{that}} \\ $$ $$\underset{\boldsymbol{{k}}=\mathrm{0}} {\overset{+\infty} {\sum}}\boldsymbol{{k}}^{\mathrm{2}} \boldsymbol{{q}}^{\boldsymbol{{k}}} =\frac{\boldsymbol{{q}}^{\mathrm{2}} +\boldsymbol{{q}}}{\left(\mathrm{1}−\boldsymbol{{q}}\right)^{\mathrm{3}} } \\ $$
Answered by Dwaipayan Shikari last updated on 30/Jan/21
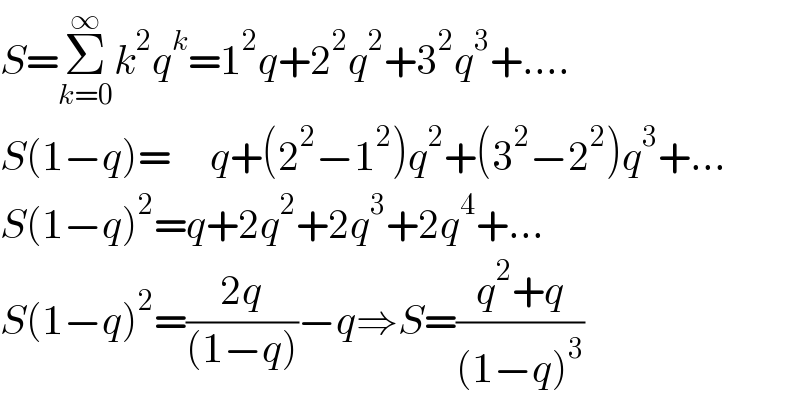
$${S}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{k}^{\mathrm{2}} {q}^{{k}} =\mathrm{1}^{\mathrm{2}} {q}+\mathrm{2}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} {q}^{\mathrm{3}} +.... \\ $$ $${S}\left(\mathrm{1}−{q}\right)=\:\:\:\:\:{q}+\left(\mathrm{2}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} \right){q}^{\mathrm{2}} +\left(\mathrm{3}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} \right){q}^{\mathrm{3}} +... \\ $$ $${S}\left(\mathrm{1}−{q}\right)^{\mathrm{2}} ={q}+\mathrm{2}{q}^{\mathrm{2}} +\mathrm{2}{q}^{\mathrm{3}} +\mathrm{2}{q}^{\mathrm{4}} +... \\ $$ $${S}\left(\mathrm{1}−{q}\right)^{\mathrm{2}} =\frac{\mathrm{2}{q}}{\left(\mathrm{1}−{q}\right)}−{q}\Rightarrow{S}=\frac{{q}^{\mathrm{2}} +{q}}{\left(\mathrm{1}−{q}\right)^{\mathrm{3}} } \\ $$
