
Question Number 130845 by mnjuly1970 last updated on 29/Jan/21
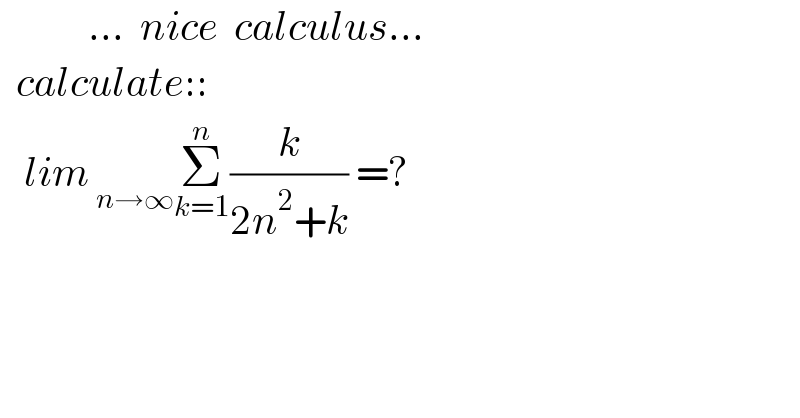
$$\:\:\:\:\:\:\:\:\:\:\:...\:\:{nice}\:\:{calculus}... \\ $$$$\:\:{calculate}:: \\ $$$$\:\:\:{lim}_{\:{n}\rightarrow\infty} \underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}}{\mathrm{2}{n}^{\mathrm{2}} +{k}}\:=? \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 29/Jan/21
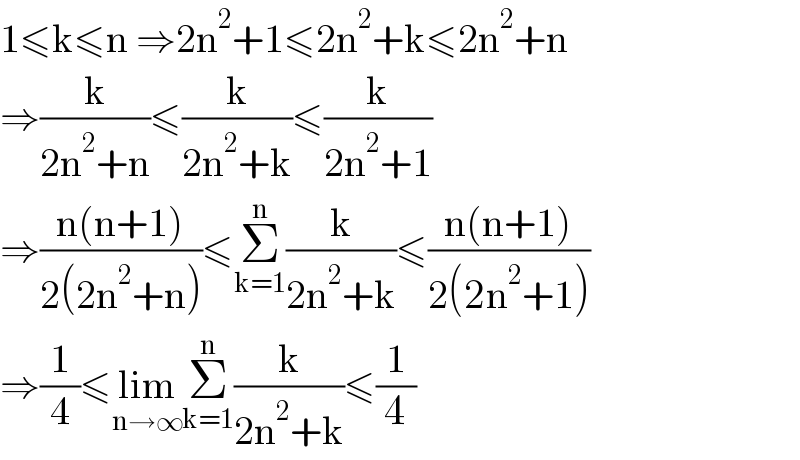
$$\mathrm{1}\leqslant\mathrm{k}\leqslant\mathrm{n}\:\Rightarrow\mathrm{2n}^{\mathrm{2}} +\mathrm{1}\leqslant\mathrm{2n}^{\mathrm{2}} +\mathrm{k}\leqslant\mathrm{2n}^{\mathrm{2}} +\mathrm{n} \\ $$$$\Rightarrow\frac{\mathrm{k}}{\mathrm{2n}^{\mathrm{2}} +\mathrm{n}}\leqslant\frac{\mathrm{k}}{\mathrm{2n}^{\mathrm{2}} +\mathrm{k}}\leqslant\frac{\mathrm{k}}{\mathrm{2n}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{2n}^{\mathrm{2}} +\mathrm{n}\right)}\leqslant\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{k}}{\mathrm{2n}^{\mathrm{2}} +\mathrm{k}}\leqslant\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{2n}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\leqslant\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{k}}{\mathrm{2n}^{\mathrm{2}} +\mathrm{k}}\leqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 29/Jan/21
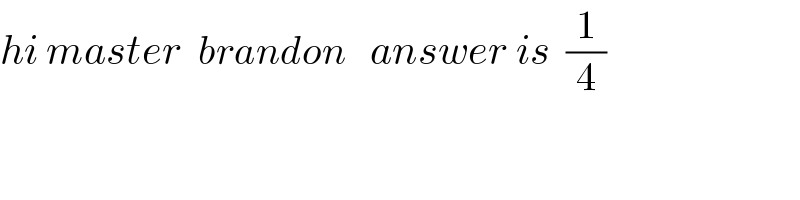
$${hi}\:{master}\:\:{brandon}\:\:\:{answer}\:{is}\:\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 29/Jan/21
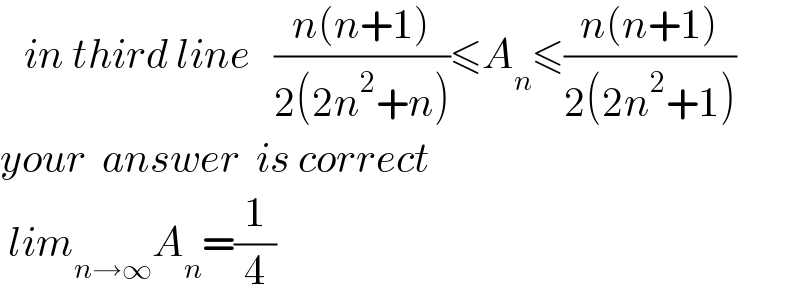
$$\:\:\:{in}\:{third}\:{line}\:\:\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{2}{n}^{\mathrm{2}} +{n}\right)}\leqslant{A}_{{n}} \leqslant\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{1}\right)}\:\: \\ $$$${your}\:\:{answer}\:\:{is}\:{correct} \\ $$$$\:{lim}_{{n}\rightarrow\infty} {A}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by Ar Brandon last updated on 29/Jan/21
$$\mathrm{Oh}!\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{remark},\:\mathrm{Sir} \\ $$😃
