
Question Number 130818 by Study last updated on 29/Jan/21
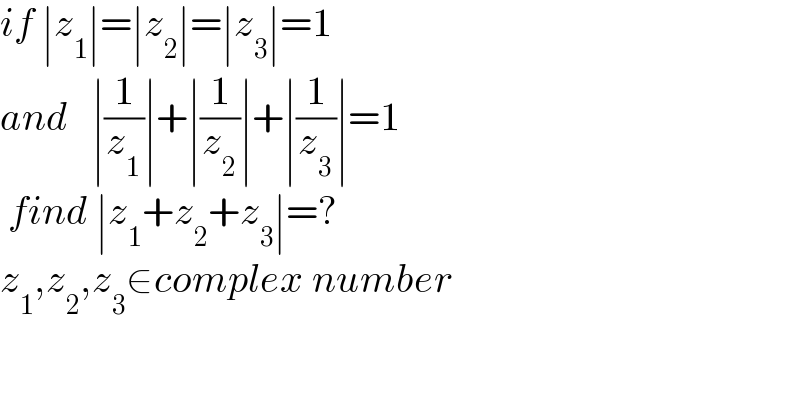
$${if}\:\mid{z}_{\mathrm{1}} \mid=\mid{z}_{\mathrm{2}} \mid=\mid{z}_{\mathrm{3}} \mid=\mathrm{1}\:\: \\ $$$${and}\:\:\:\mid\frac{\mathrm{1}}{{z}_{\mathrm{1}} }\mid+\mid\frac{\mathrm{1}}{{z}_{\mathrm{2}} }\mid+\mid\frac{\mathrm{1}}{{z}_{\mathrm{3}} }\mid=\mathrm{1} \\ $$$$\:{find}\:\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} +{z}_{\mathrm{3}} \mid=?\:\:\: \\ $$$${z}_{\mathrm{1}} ,{z}_{\mathrm{2}} ,{z}_{\mathrm{3}} \in{complex}\:{number} \\ $$
Answered by TheSupreme last updated on 29/Jan/21
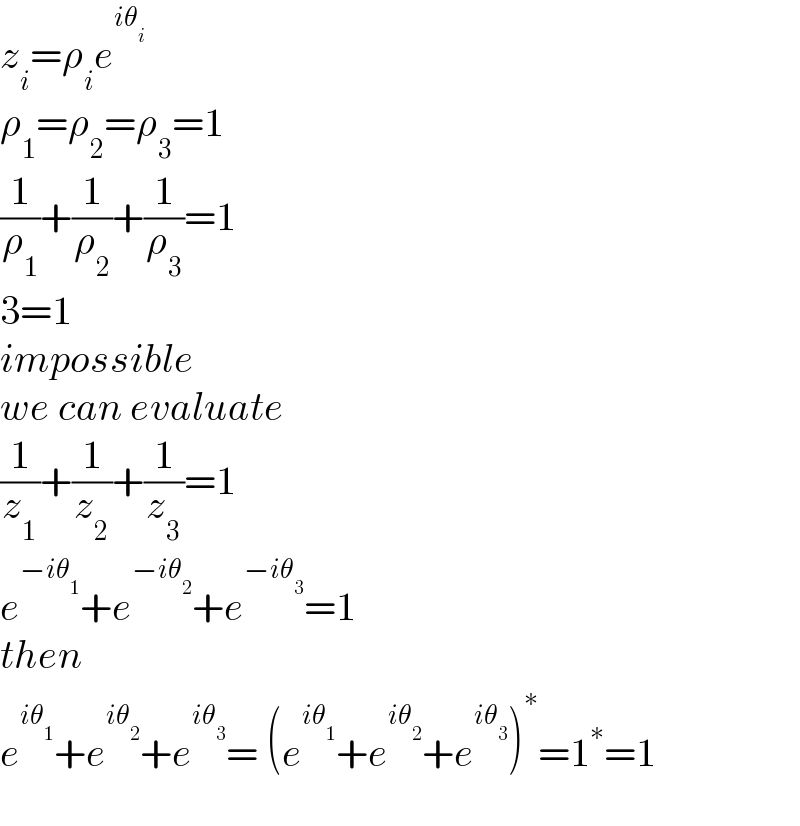
$${z}_{{i}} =\rho_{{i}} {e}^{{i}\theta_{{i}} } \\ $$$$\rho_{\mathrm{1}} =\rho_{\mathrm{2}} =\rho_{\mathrm{3}} =\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\rho_{\mathrm{1}} }+\frac{\mathrm{1}}{\rho_{\mathrm{2}} }+\frac{\mathrm{1}}{\rho_{\mathrm{3}} }=\mathrm{1}\: \\ $$$$\mathrm{3}=\mathrm{1} \\ $$$${impossible} \\ $$$${we}\:{can}\:{evaluate} \\ $$$$\frac{\mathrm{1}}{{z}_{\mathrm{1}} }+\frac{\mathrm{1}}{{z}_{\mathrm{2}} }+\frac{\mathrm{1}}{{z}_{\mathrm{3}} }=\mathrm{1} \\ $$$${e}^{−{i}\theta_{\mathrm{1}} } +{e}^{−{i}\theta_{\mathrm{2}} } +{e}^{−{i}\theta_{\mathrm{3}} } =\mathrm{1} \\ $$$${then} \\ $$$${e}^{{i}\theta_{\mathrm{1}} } +{e}^{{i}\theta_{\mathrm{2}} } +{e}^{{i}\theta_{\mathrm{3}} } =\:\left({e}^{{i}\theta_{\mathrm{1}} } +{e}^{{i}\theta_{\mathrm{2}} } +{e}^{{i}\theta_{\mathrm{3}} } \right)^{\ast} =\mathrm{1}^{\ast} =\mathrm{1} \\ $$$$ \\ $$
Commented by Study last updated on 30/Jan/21

$${thanks}\:{sir} \\ $$
