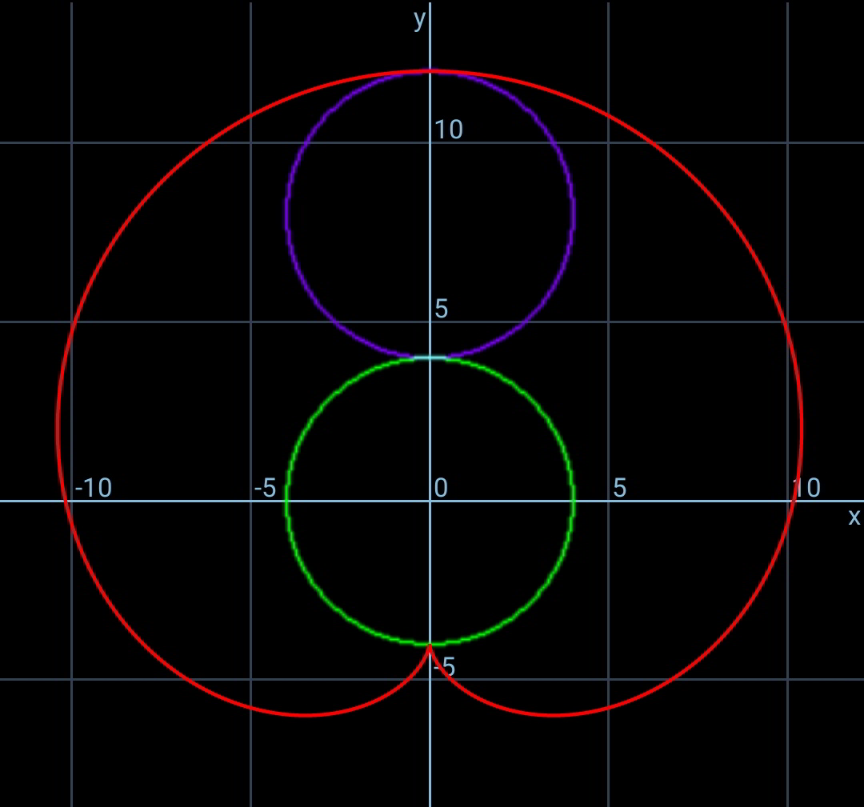
Question Number 130795 by mr W last updated on 29/Jan/21

Commented by mr W last updated on 29/Jan/21
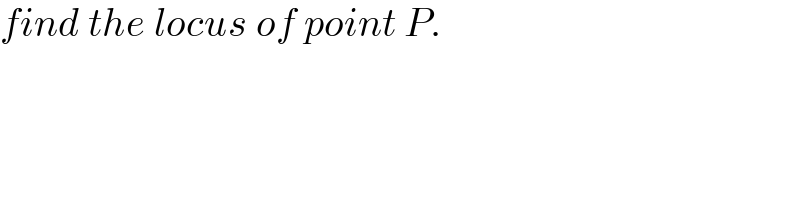
$${find}\:{the}\:{locus}\:{of}\:{point}\:{P}. \\ $$
Answered by mr W last updated on 29/Jan/21
Commented by mr W last updated on 29/Jan/21
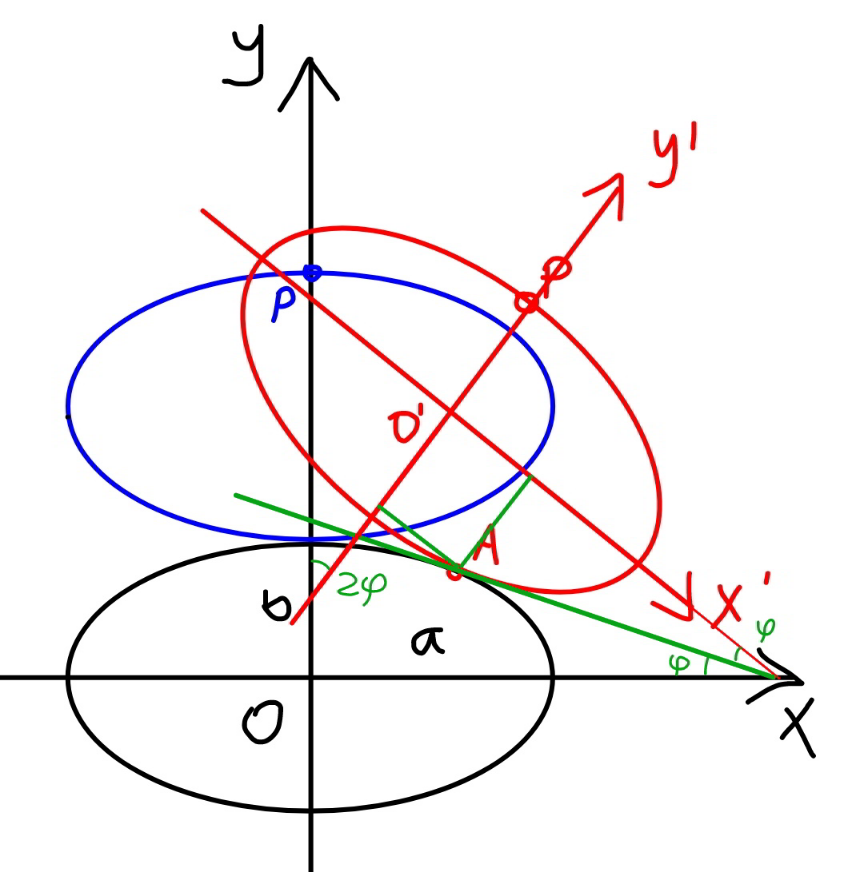
![μ=(b/a) say A(a cos θ, b sin θ) tan ϕ=((b cos θ)/(a sin θ))=(μ/(tan θ)) ⇒ϕ=tan^(−1) ((μ/(tan θ))) x_P =a cos θ−a cos θ cos 2ϕ+b(1+sin θ) sin 2ϕ ⇒x_P =a[cos θ (1−cos 2ϕ)+μ(1+sin θ) sin 2ϕ] y_P =b sin θ+a cos θ sin 2ϕ+b(1+sin θ) cos 2ϕ ⇒y_P =a[μ sin θ+cos θ sin 2ϕ+μ(1+sin θ) cos 2ϕ]](Q130831.png)
$$\mu=\frac{{b}}{{a}} \\ $$$${say}\:{A}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{tan}\:\varphi=\frac{{b}\:\mathrm{cos}\:\theta}{{a}\:\mathrm{sin}\:\theta}=\frac{\mu}{\mathrm{tan}\:\theta} \\ $$$$\Rightarrow\varphi=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mu}{\mathrm{tan}\:\theta}\right) \\ $$$${x}_{{P}} ={a}\:\mathrm{cos}\:\theta−{a}\:\mathrm{cos}\:\theta\:\mathrm{cos}\:\mathrm{2}\varphi+{b}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\:\mathrm{sin}\:\mathrm{2}\varphi \\ $$$$\Rightarrow{x}_{{P}} ={a}\left[\mathrm{cos}\:\theta\:\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\varphi\right)+\mu\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\:\mathrm{sin}\:\mathrm{2}\varphi\right] \\ $$$${y}_{{P}} ={b}\:\mathrm{sin}\:\theta+{a}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\mathrm{2}\varphi+{b}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\:\mathrm{cos}\:\mathrm{2}\varphi \\ $$$$\Rightarrow{y}_{{P}} ={a}\left[\mu\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\mathrm{sin}\:\mathrm{2}\varphi+\mu\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\:\mathrm{cos}\:\mathrm{2}\varphi\right] \\ $$
Commented by mr W last updated on 29/Jan/21

Commented by mr W last updated on 29/Jan/21
Commented by mr W last updated on 29/Jan/21