
Question Number 130781 by EDWIN88 last updated on 28/Jan/21
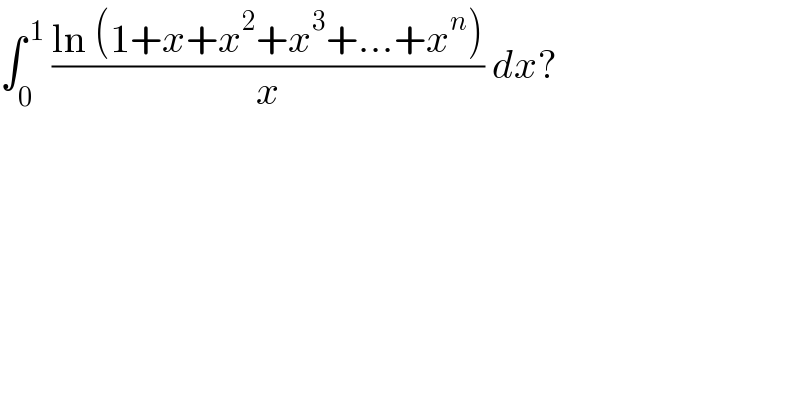
$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...+{x}^{{n}} \right)}{{x}}\:{dx}? \\ $$
Answered by mathmax by abdo last updated on 29/Jan/21
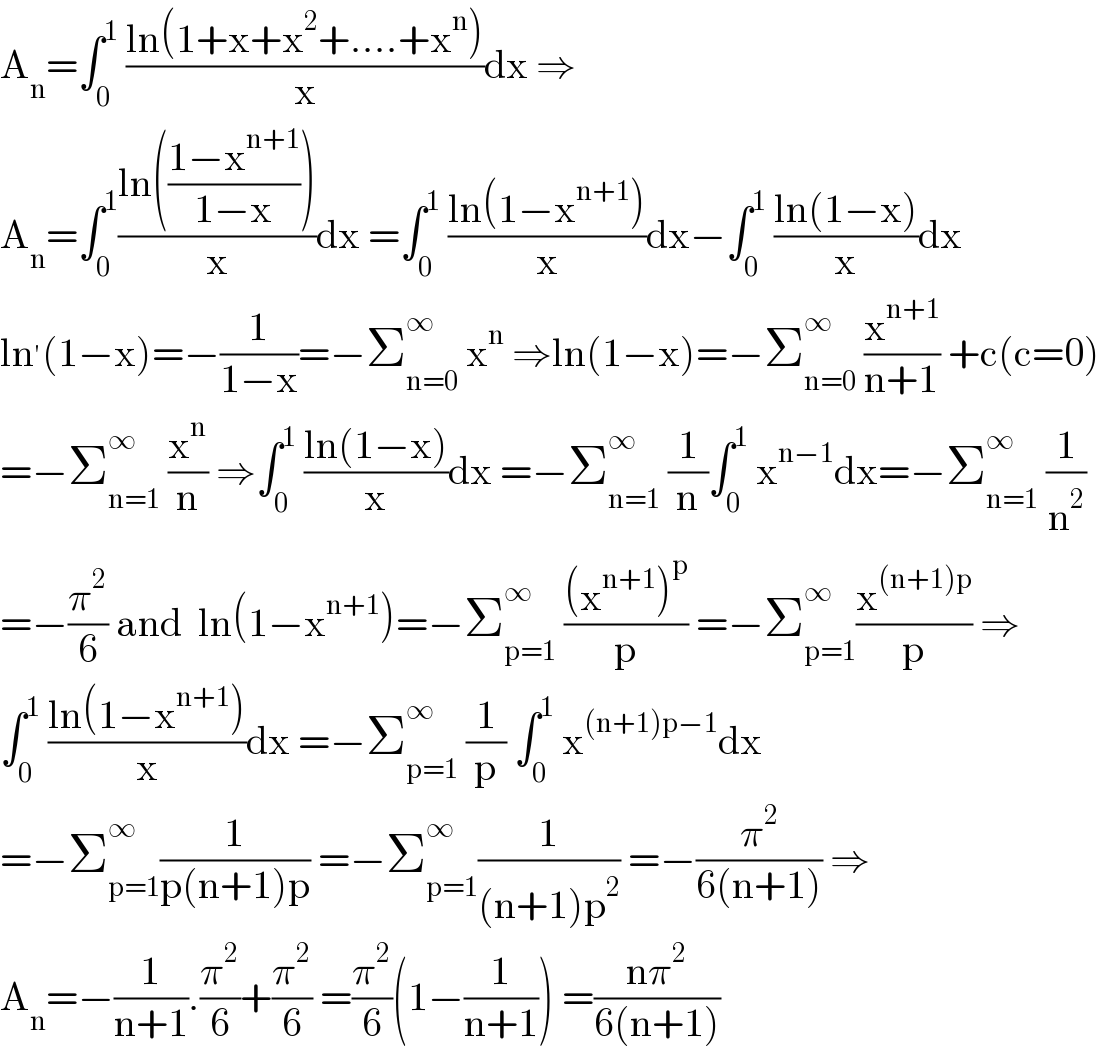
$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} +....+\mathrm{x}^{\mathrm{n}} \right)}{\mathrm{x}}\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\frac{\mathrm{1}−\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{1}−\mathrm{x}}\right)}{\mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{n}+\mathrm{1}} \right)}{\mathrm{x}}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{ln}^{'} \left(\mathrm{1}−\mathrm{x}\right)=−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:+\mathrm{c}\left(\mathrm{c}=\mathrm{0}\right) \\ $$$$=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{dx}=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} } \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\mathrm{and}\:\:\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{n}+\mathrm{1}} \right)=−\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \:\frac{\left(\mathrm{x}^{\mathrm{n}+\mathrm{1}} \right)^{\mathrm{p}} }{\mathrm{p}}\:=−\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \frac{\mathrm{x}^{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{p}} }{\mathrm{p}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{n}+\mathrm{1}} \right)}{\mathrm{x}}\mathrm{dx}\:=−\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{p}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{p}−\mathrm{1}} \mathrm{dx} \\ $$$$=−\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{p}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{p}}\:=−\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{p}^{\mathrm{2}} }\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}\left(\mathrm{n}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)\:=\frac{\mathrm{n}\pi^{\mathrm{2}} }{\mathrm{6}\left(\mathrm{n}+\mathrm{1}\right)} \\ $$
Commented by mathmax by abdo last updated on 29/Jan/21
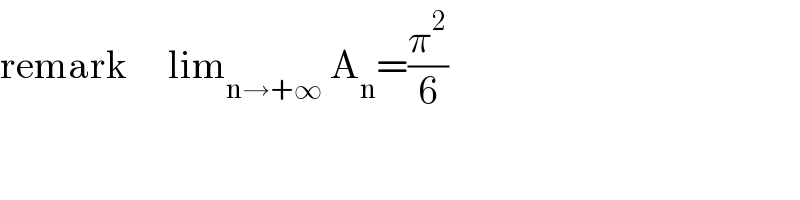
$$\mathrm{remark}\:\:\:\:\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Commented by Lordose last updated on 29/Jan/21

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{sir} \\ $$
Answered by mnjuly1970 last updated on 29/Jan/21
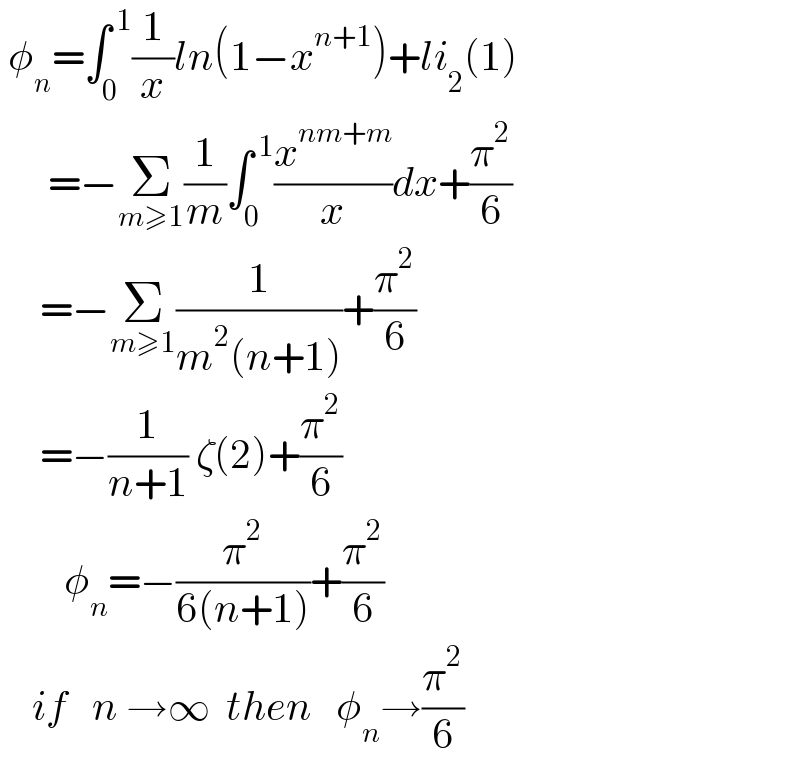
$$\:\phi_{{n}} =\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}−{x}^{{n}+\mathrm{1}} \right)+{li}_{\mathrm{2}} \left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:=−\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{m}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{nm}+{m}} }{{x}}{dx}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\:\:\:\:\:=−\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{m}^{\mathrm{2}} \left({n}+\mathrm{1}\right)}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\zeta\left(\mathrm{2}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\phi_{{n}} =−\frac{\pi^{\mathrm{2}} }{\mathrm{6}\left({n}+\mathrm{1}\right)}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\:\:\:\:{if}\:\:\:{n}\:\rightarrow\infty\:\:{then}\:\:\:\phi_{{n}} \rightarrow\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Answered by Dwaipayan Shikari last updated on 29/Jan/21
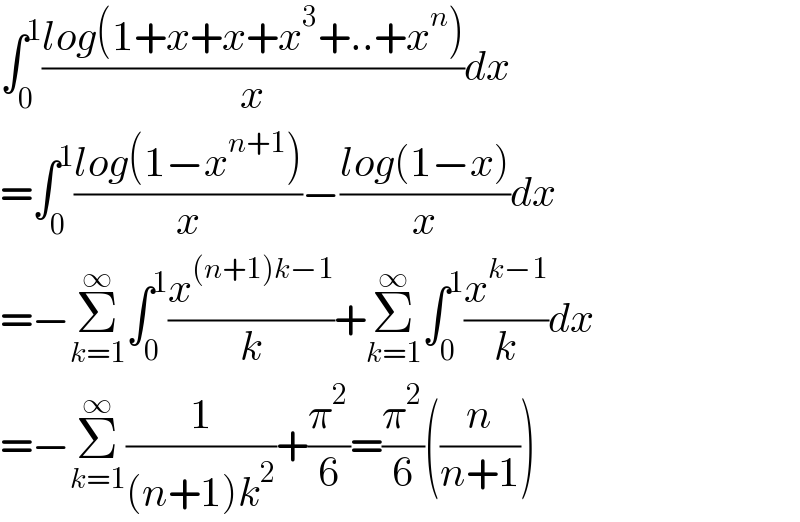
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{x}+{x}+{x}^{\mathrm{3}} +..+{x}^{{n}} \right)}{{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}−{x}^{{n}+\mathrm{1}} \right)}{{x}}−\frac{{log}\left(\mathrm{1}−{x}\right)}{{x}}{dx} \\ $$$$=−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\left({n}+\mathrm{1}\right){k}−\mathrm{1}} }{{k}}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{k}−\mathrm{1}} }{{k}}{dx} \\ $$$$=−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right){k}^{\mathrm{2}} }+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\left(\frac{{n}}{{n}+\mathrm{1}}\right) \\ $$
