
Question Number 130738 by bemath last updated on 28/Jan/21
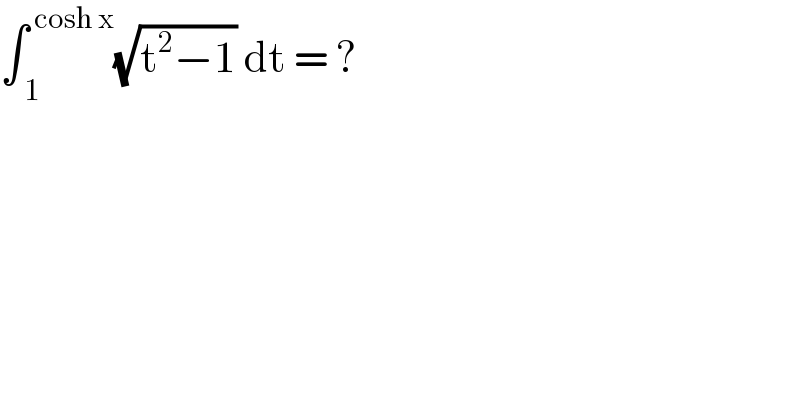
$$\int_{\:\mathrm{1}} ^{\:\mathrm{cosh}\:\mathrm{x}} \sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{dt}\:=\:?\: \\ $$
Answered by MJS_new last updated on 28/Jan/21
![∫(√(t^2 −1))dt= [t=cosh u ⇔ u=cosh^(−1) t → dt=sinh u du] =∫sinh^2 u du=−(1/2)(u−sinh u cosh u)= =−(1/2)(cosh^(−1) t −t(√(t^2 −1)))+C ⇒ answer is −((x−sinh x cosh x)/2)](Q130749.png)
$$\int\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{cosh}\:{u}\:\Leftrightarrow\:{u}=\mathrm{cosh}^{−\mathrm{1}} \:{t}\:\rightarrow\:{dt}=\mathrm{sinh}\:{u}\:{du}\right] \\ $$$$=\int\mathrm{sinh}^{\mathrm{2}} \:{u}\:{du}=−\frac{\mathrm{1}}{\mathrm{2}}\left({u}−\mathrm{sinh}\:{u}\:\mathrm{cosh}\:{u}\right)= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cosh}^{−\mathrm{1}} \:{t}\:−{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:−\frac{{x}−\mathrm{sinh}\:{x}\:\mathrm{cosh}\:{x}}{\mathrm{2}} \\ $$
Commented by bemath last updated on 29/Jan/21

$$\mathrm{great} \\ $$
Answered by mathmax by abdo last updated on 28/Jan/21
![f(x)=∫_1 ^(ch(x)) (√(t^2 −1))dt we do the changement t=chz ⇒ f(x)=∫_0 ^x shz shz dz =∫_0 ^x ((ch(2z)−1)/2)dz =(1/4)sh(2z)]_0 ^x −(x/2) =(1/4)sh(2x)−(x/2) .](Q130767.png)
$$\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{1}} ^{\mathrm{ch}\left(\mathrm{x}\right)} \sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{t}=\mathrm{chz}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{x}} \mathrm{shz}\:\mathrm{shz}\:\mathrm{dz}\:=\int_{\mathrm{0}} ^{\mathrm{x}} \frac{\mathrm{ch}\left(\mathrm{2z}\right)−\mathrm{1}}{\mathrm{2}}\mathrm{dz} \\ $$$$\left.=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sh}\left(\mathrm{2z}\right)\right]_{\mathrm{0}} ^{\mathrm{x}} −\frac{\mathrm{x}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sh}\left(\mathrm{2x}\right)−\frac{\mathrm{x}}{\mathrm{2}}\:. \\ $$
Commented by bemath last updated on 29/Jan/21

$$\mathrm{nice} \\ $$
