Question Number 13067 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/May/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/May/17
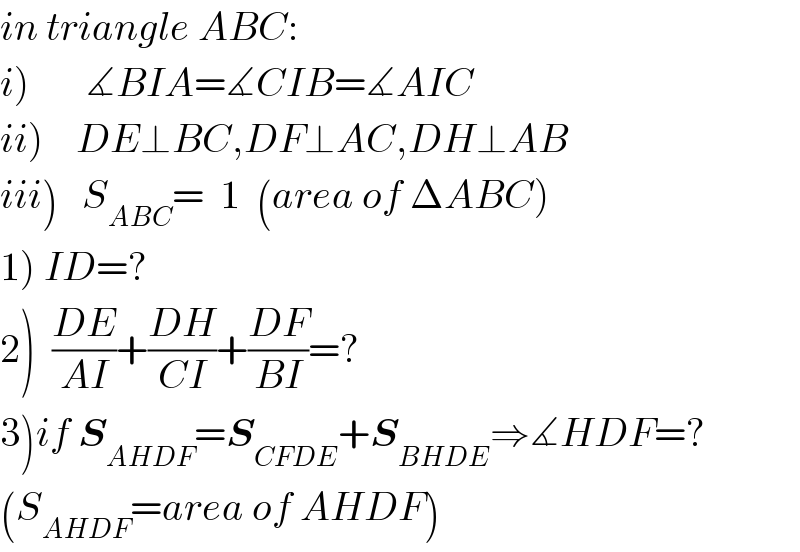
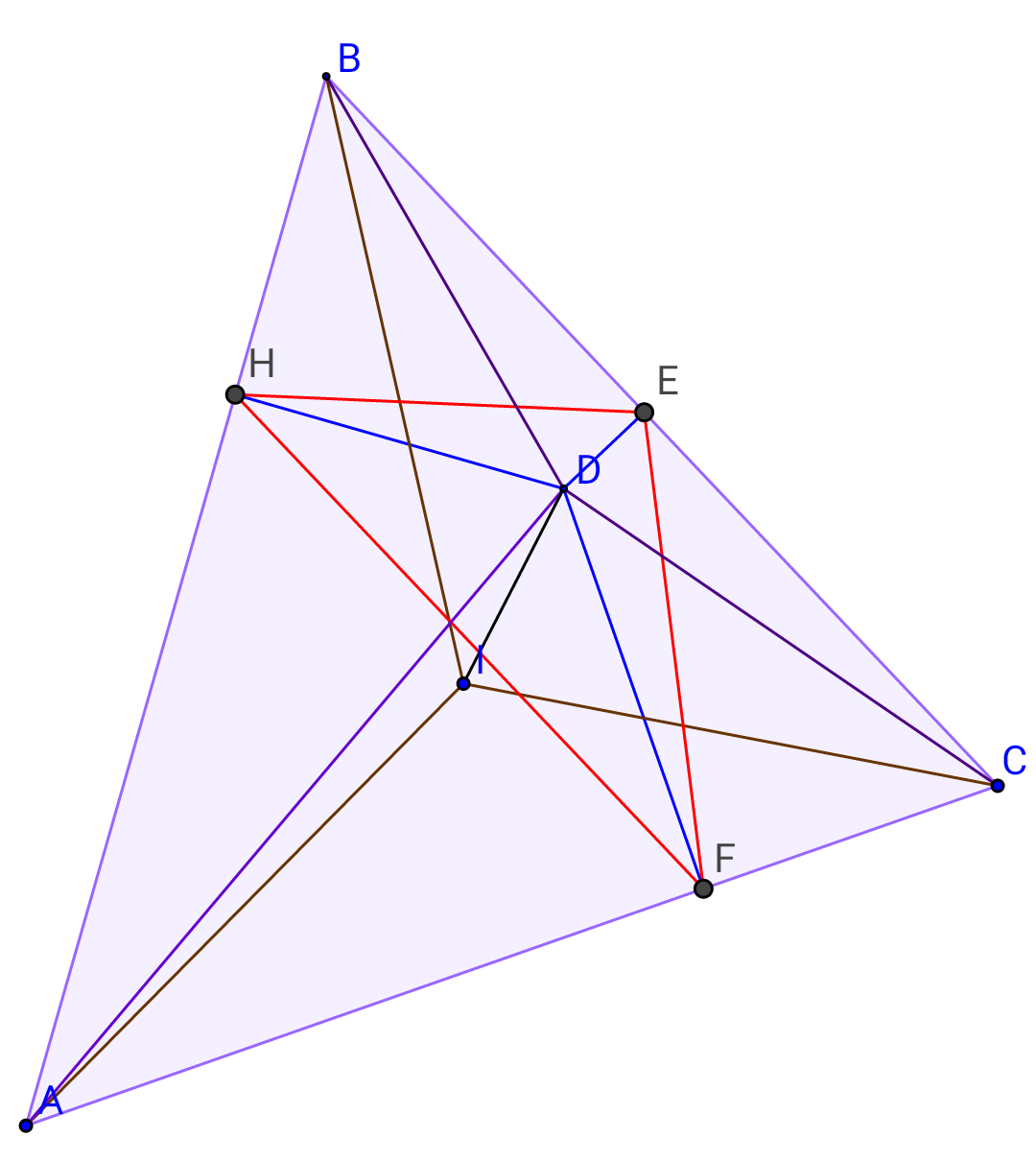
$${in}\:{triangle}\:{ABC}: \\ $$$$\left.{i}\right)\:\:\:\:\:\:\:\measuredangle{BIA}=\measuredangle{CIB}=\measuredangle{AIC} \\ $$$$\left.{ii}\right)\:\:\:\:{DE}\bot{BC},{DF}\bot{AC},{DH}\bot{AB} \\ $$$$\left.{iii}\right)\:\:\:{S}_{{ABC}} =\:\:\mathrm{1}\:\:\left({area}\:{of}\:\Delta{ABC}\right) \\ $$$$\left.\mathrm{1}\right)\:{ID}=? \\ $$$$\left.\mathrm{2}\right)\:\:\frac{{DE}}{{AI}}+\frac{{DH}}{{CI}}+\frac{{DF}}{{BI}}=? \\ $$$$\left.\mathrm{3}\right){if}\:\boldsymbol{{S}}_{{AHDF}} =\boldsymbol{{S}}_{{CFDE}} +\boldsymbol{{S}}_{{BHDE}} \Rightarrow\measuredangle{HDF}=? \\ $$$$\left({S}_{{AHDF}} ={area}\:{of}\:{AHDF}\right) \\ $$
Commented by mrW1 last updated on 13/May/17

$${The}\:{position}\:{of}\:{I}\:{is}\:{uniquely}\:{defined}, \\ $$$${but}\:{the}\:{position}\:{of}\:{D}\:{is}\:{not}\:{uniquely} \\ $$$${defined},\:{therefore}\:{ID}\:{could}\:{be}\:{any} \\ $$$${value}. \\ $$$$ \\ $$$$\measuredangle{HDF}=\mathrm{180}°−\measuredangle{A},\:{this}\:{is}\:{always}\:{true}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/May/17
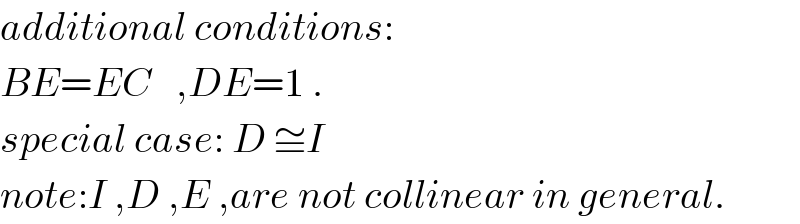
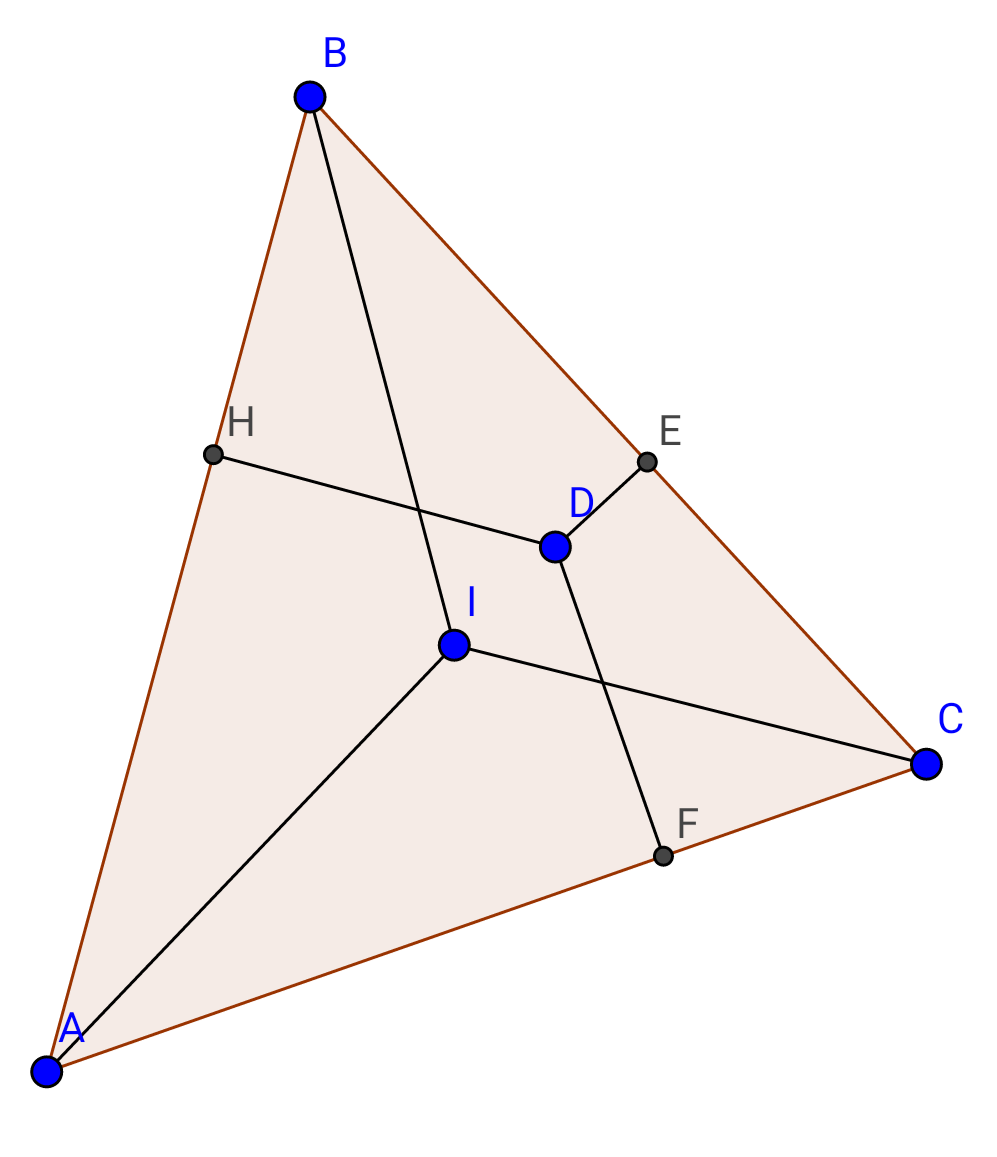
$${additional}\:{conditions}: \\ $$$${BE}={EC}\:\:\:,{DE}=\mathrm{1}\:. \\ $$$${special}\:{case}:\:{D}\:\cong{I} \\ $$$${note}:{I}\:,{D}\:,{E}\:,{are}\:{not}\:{collinear}\:{in}\:{general}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/May/17