
Question Number 130589 by bramlexs22 last updated on 27/Jan/21
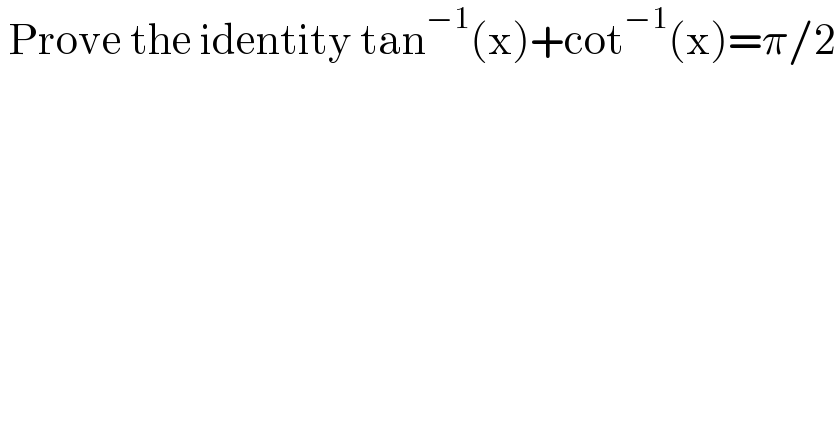
$$\:\mathrm{Prove}\:\mathrm{the}\:\mathrm{identity}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)+\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{x}\right)=\pi/\mathrm{2} \\ $$
Answered by EDWIN88 last updated on 27/Jan/21
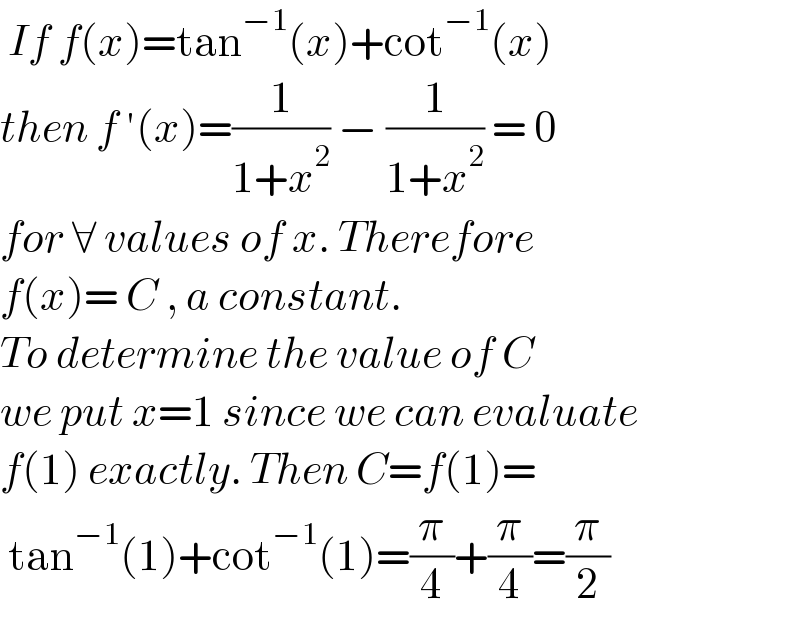
$$\:{If}\:{f}\left({x}\right)=\mathrm{tan}^{−\mathrm{1}} \left({x}\right)+\mathrm{cot}^{−\mathrm{1}} \left({x}\right) \\ $$$${then}\:{f}\:'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$${for}\:\forall\:{values}\:{of}\:{x}.\:{Therefore}\: \\ $$$${f}\left({x}\right)=\:{C}\:,\:{a}\:{constant}. \\ $$$${To}\:{determine}\:{the}\:{value}\:{of}\:{C} \\ $$$${we}\:{put}\:{x}=\mathrm{1}\:{since}\:{we}\:{can}\:{evaluate} \\ $$$${f}\left(\mathrm{1}\right)\:{exactly}.\:{Then}\:{C}={f}\left(\mathrm{1}\right)= \\ $$$$\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)+\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{2}} \\ $$
