
Question Number 130512 by MJS_new last updated on 26/Jan/21
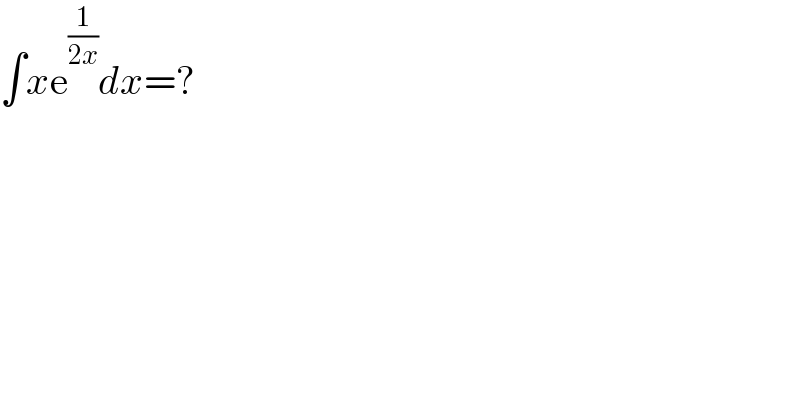
$$\int{x}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{x}}} {dx}=? \\ $$
Commented by Dwaipayan Shikari last updated on 26/Jan/21

$$\frac{\mathrm{1}}{\mathrm{2}{x}}=−{t}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }=\frac{{dt}}{{dx}} \\ $$$$=−\mathrm{2}\int{x}^{\mathrm{3}} {e}^{−{t}} {dt}=−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{e}^{−{t}} }{{t}^{\mathrm{3}} }{dt}=−\int\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{t}^{\mathrm{3}} }−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}{t}}−\frac{\mathrm{1}}{\mathrm{6}}+\frac{{t}}{\mathrm{24}}−\frac{{t}^{\mathrm{2}} }{\mathrm{120}}...\right){dt} \\ $$$$=−\left(−\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}{t}}+\frac{\mathrm{1}}{\mathrm{8}}{log}\left({t}\right)−\frac{{t}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{t}}{\mathrm{24}}−\frac{{t}^{\mathrm{2}} }{\mathrm{120}}+\frac{{t}^{\mathrm{3}} }{\mathrm{720}}−\frac{{t}^{\mathrm{4}} }{\mathrm{5040}}+..\right) \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4}{t}}+\frac{{t}}{\mathrm{6}}−\frac{{t}^{\mathrm{2}} }{\mathrm{192}}+\frac{{t}^{\mathrm{3}} }{\mathrm{1440}}+...\right)−\frac{\mathrm{1}}{\mathrm{8}}{log}\left({t}\right)+{C} \\ $$$$=+\left(\frac{\mathrm{1}}{{t}^{\mathrm{3}} }.\frac{{t}}{\mathrm{2}}+\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\left(\frac{{t}}{\mathrm{2}}\right)\left(−\frac{{t}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\left(\frac{{t}}{\mathrm{2}}\right)\left(−\frac{{t}}{\mathrm{2}}\right)\left(\frac{−\mathrm{2}{t}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\left(\frac{{t}}{\mathrm{2}}\right)\left(−\frac{{t}}{\mathrm{2}}\right)\left(\frac{−\mathrm{2}{t}}{\mathrm{3}}\right)\left(−\frac{{t}}{\mathrm{32}}\right)+...\right)−\frac{\mathrm{1}}{\mathrm{8}}{log}\left({t}\right) \\ $$$$=\frac{\frac{\mathrm{1}}{{t}^{\mathrm{3}} }}{\mathrm{1}−\frac{\frac{{t}}{\mathrm{2}}}{\mathrm{1}+\frac{{t}}{\mathrm{2}}+\frac{\frac{{t}}{\mathrm{2}}}{\mathrm{1}−\frac{{t}}{\mathrm{2}}+\frac{\frac{\mathrm{2}{t}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{2}{t}}{\mathrm{3}}+\frac{\frac{{t}}{\mathrm{32}}}{\mathrm{1}−\frac{{t}}{\mathrm{32}}+...}}}}}−\frac{\mathrm{1}}{\mathrm{8}}{log}\left({t}\right)+{C} \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{2}{x}}\:\: \\ $$
Commented by Dwaipayan Shikari last updated on 26/Jan/21
https://en.wikipedia.org/wiki/Euler%27s_continued_fraction_formula I have learnt it from here
Answered by Ar Brandon last updated on 26/Jan/21
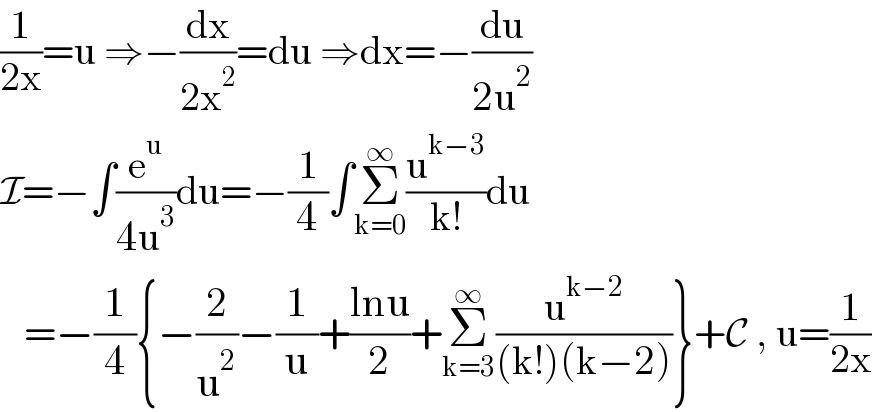
$$\frac{\mathrm{1}}{\mathrm{2x}}=\mathrm{u}\:\Rightarrow−\frac{\mathrm{dx}}{\mathrm{2x}^{\mathrm{2}} }=\mathrm{du}\:\Rightarrow\mathrm{dx}=−\frac{\mathrm{du}}{\mathrm{2u}^{\mathrm{2}} } \\ $$$$\mathcal{I}=−\int\frac{\mathrm{e}^{\mathrm{u}} }{\mathrm{4u}^{\mathrm{3}} }\mathrm{du}=−\frac{\mathrm{1}}{\mathrm{4}}\int\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{u}^{\mathrm{k}−\mathrm{3}} }{\mathrm{k}!}\mathrm{du} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{4}}\left\{−\frac{\mathrm{2}}{\mathrm{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{u}}+\frac{\mathrm{lnu}}{\mathrm{2}}+\underset{\mathrm{k}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\mathrm{u}^{\mathrm{k}−\mathrm{2}} }{\left(\mathrm{k}!\right)\left(\mathrm{k}−\mathrm{2}\right)}\right\}+\mathcal{C}\:,\:\mathrm{u}=\frac{\mathrm{1}}{\mathrm{2x}} \\ $$
Commented by MJS_new last updated on 26/Jan/21
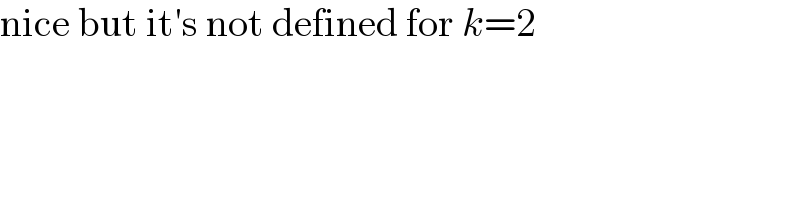
$$\mathrm{nice}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:{k}=\mathrm{2} \\ $$
Commented by Ar Brandon last updated on 26/Jan/21
You're right Sir
Answered by MJS_new last updated on 26/Jan/21
![∫xe^(1/(2x)) dx= [t=(1/(2x)) → dx=−2x^2 dt] =−(1/4)∫(e^t /t^3 )dt [by parts] =(e^t /(8t^2 ))−(1/8)∫(e^t /t^2 )dt= [by parts] =(e^t /(8t^2 ))+(e^t /(8t))−(1/8)∫(e^t /t)dt= =(e^t /(8t^2 ))+(e^t /(8t))−(1/8)Ei (t) = =(1/4)x(2x+1)e^(1/(2x)) −(1/8)Ei ((1/(2x))) +C](Q130524.png)
$$\int{x}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{x}}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{1}}{\mathrm{2}{x}}\:\rightarrow\:{dx}=−\mathrm{2}{x}^{\mathrm{2}} {dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{e}^{{t}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$=\frac{\mathrm{e}^{{t}} }{\mathrm{8}{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{e}^{{t}} }{{t}^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$=\frac{\mathrm{e}^{{t}} }{\mathrm{8}{t}^{\mathrm{2}} }+\frac{\mathrm{e}^{{t}} }{\mathrm{8}{t}}−\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{e}^{{t}} }{{t}}{dt}= \\ $$$$=\frac{\mathrm{e}^{{t}} }{\mathrm{8}{t}^{\mathrm{2}} }+\frac{\mathrm{e}^{{t}} }{\mathrm{8}{t}}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{Ei}\:\left({t}\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{x}\left(\mathrm{2}{x}+\mathrm{1}\right)\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{x}}} −\frac{\mathrm{1}}{\mathrm{8}}\mathrm{Ei}\:\left(\frac{\mathrm{1}}{\mathrm{2}{x}}\right)\:+{C} \\ $$
