Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 130431 by mnjuly1970 last updated on 25/Jan/21

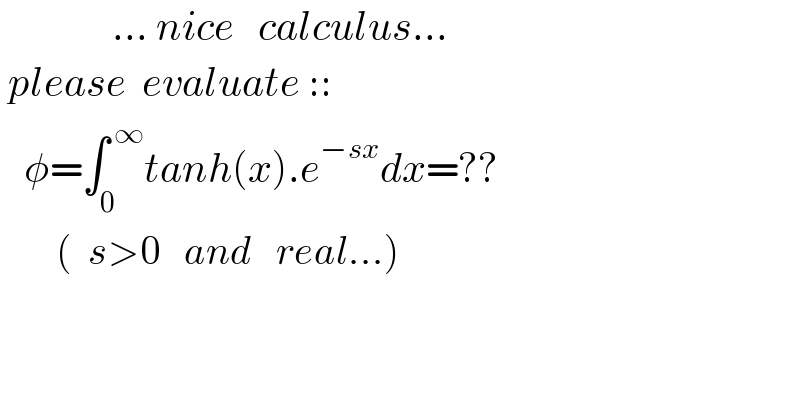
... nice calculus... please evaluate :: φ=∫_0 ^( ∞) tanh(x).e^(−sx) dx=?? ( s>0 and real...)

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\:{nice}\:\:\:{calculus}... \\ $$ $$\:{please}\:\:{evaluate}\::: \\ $$ $$\:\:\:\phi=\int_{\mathrm{0}} ^{\:\infty} {tanh}\left({x}\right).{e}^{−{sx}} {dx}=?? \\ $$ $$\:\:\:\:\:\:\:\left(\:\:{s}>\mathrm{0}\:\:\:{and}\:\:\:{real}...\right) \\ $$

Answered by Dwaipayan Shikari last updated on 25/Jan/21

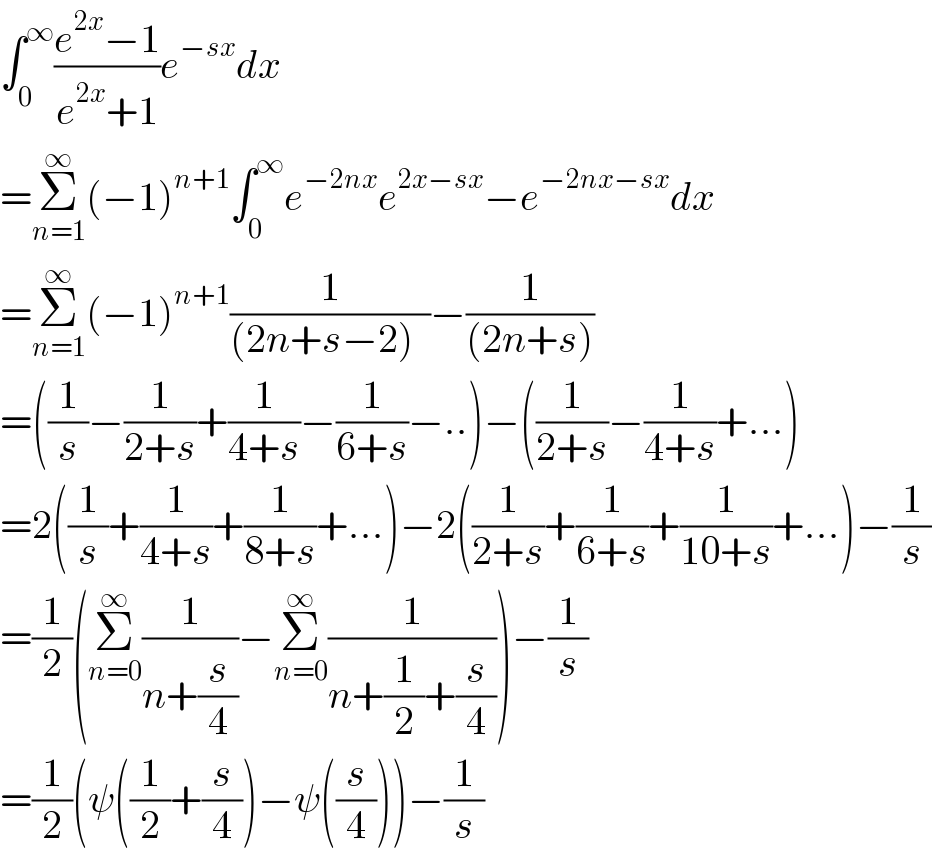
∫_0 ^∞ ((e^(2x) −1)/(e^(2x) +1))e^(−sx) dx =Σ_(n=1) ^∞ (−1)^(n+1) ∫_0 ^∞ e^(−2nx) e^(2x−sx) −e^(−2nx−sx) dx =Σ_(n=1) ^∞ (−1)^(n+1) (1/((2n+s−2) ))−(1/((2n+s))) =((1/s)−(1/(2+s))+(1/(4+s))−(1/(6+s))−..)−((1/(2+s))−(1/(4+s))+...) =2((1/s)+(1/(4+s))+(1/(8+s))+...)−2((1/(2+s))+(1/(6+s))+(1/(10+s))+...)−(1/s) =(1/2)(Σ_(n=0) ^∞ (1/(n+(s/4)))−Σ_(n=0) ^∞ (1/(n+(1/2)+(s/4))))−(1/s) =(1/2)(ψ((1/2)+(s/4))−ψ((s/4)))−(1/s)

$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{{e}^{\mathrm{2}{x}} +\mathrm{1}}{e}^{−{sx}} {dx} \\ $$ $$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{nx}} {e}^{\mathrm{2}{x}−{sx}} −{e}^{−\mathrm{2}{nx}−{sx}} {dx}\:\:\:\:\:\:\: \\ $$ $$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{2}{n}+{s}−\mathrm{2}\right)\:\:}−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+{s}\right)} \\ $$ $$=\left(\frac{\mathrm{1}}{{s}}−\frac{\mathrm{1}}{\mathrm{2}+{s}}+\frac{\mathrm{1}}{\mathrm{4}+{s}}−\frac{\mathrm{1}}{\mathrm{6}+{s}}−..\right)−\left(\frac{\mathrm{1}}{\mathrm{2}+{s}}−\frac{\mathrm{1}}{\mathrm{4}+{s}}+...\right) \\ $$ $$=\mathrm{2}\left(\frac{\mathrm{1}}{{s}}+\frac{\mathrm{1}}{\mathrm{4}+{s}}+\frac{\mathrm{1}}{\mathrm{8}+{s}}+...\right)−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}+{s}}+\frac{\mathrm{1}}{\mathrm{6}+{s}}+\frac{\mathrm{1}}{\mathrm{10}+{s}}+...\right)−\frac{\mathrm{1}}{{s}} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\frac{{s}}{\mathrm{4}}}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{{s}}{\mathrm{4}}}\right)−\frac{\mathrm{1}}{{s}} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}\left(\psi\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{s}}{\mathrm{4}}\right)−\psi\left(\frac{{s}}{\mathrm{4}}\right)\right)−\frac{\mathrm{1}}{{s}} \\ $$

Commented bymnjuly1970 last updated on 25/Jan/21

perfect mr payan..

$${perfect}\:{mr}\:{payan}.. \\ $$

Commented byDwaipayan Shikari last updated on 25/Jan/21

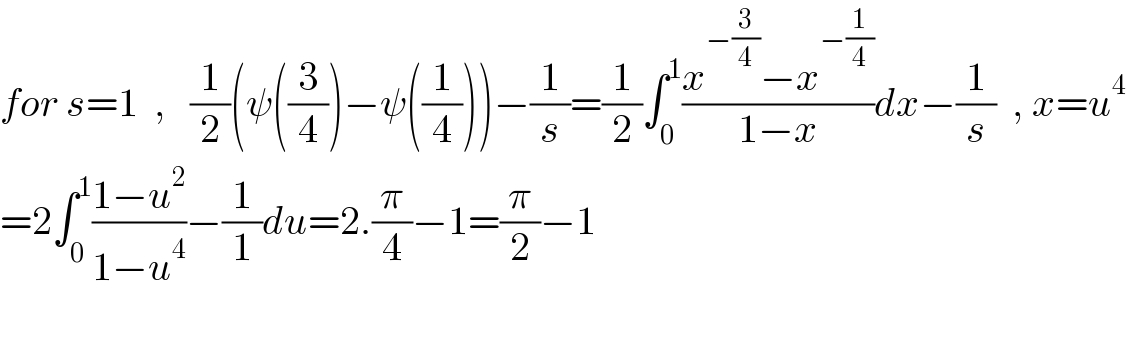
for s=1 , (1/2)(ψ((3/4))−ψ((1/4)))−(1/s)=(1/2)∫_0 ^1 ((x^(−(3/4)) −x^(−(1/4)) )/(1−x))dx−(1/s) , x=u^4 =2∫_0 ^1 ((1−u^2 )/(1−u^4 ))−(1/1)du=2.(π/4)−1=(π/2)−1

$${for}\:{s}=\mathrm{1}\:\:,\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\left(\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right)−\frac{\mathrm{1}}{{s}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{−\frac{\mathrm{3}}{\mathrm{4}}} −{x}^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\mathrm{1}−{x}}{dx}−\frac{\mathrm{1}}{{s}}\:\:,\:{x}={u}^{\mathrm{4}} \\ $$ $$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}−{u}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{1}}{du}=\mathrm{2}.\frac{\pi}{\mathrm{4}}−\mathrm{1}=\frac{\pi}{\mathrm{2}}−\mathrm{1}\:\:\:\:\:\:\: \\ $$ $$ \\ $$

Commented bymnjuly1970 last updated on 25/Jan/21

thanks alot ...

$${thanks}\:{alot}\:... \\ $$

Answered by mnjuly1970 last updated on 26/Jan/21

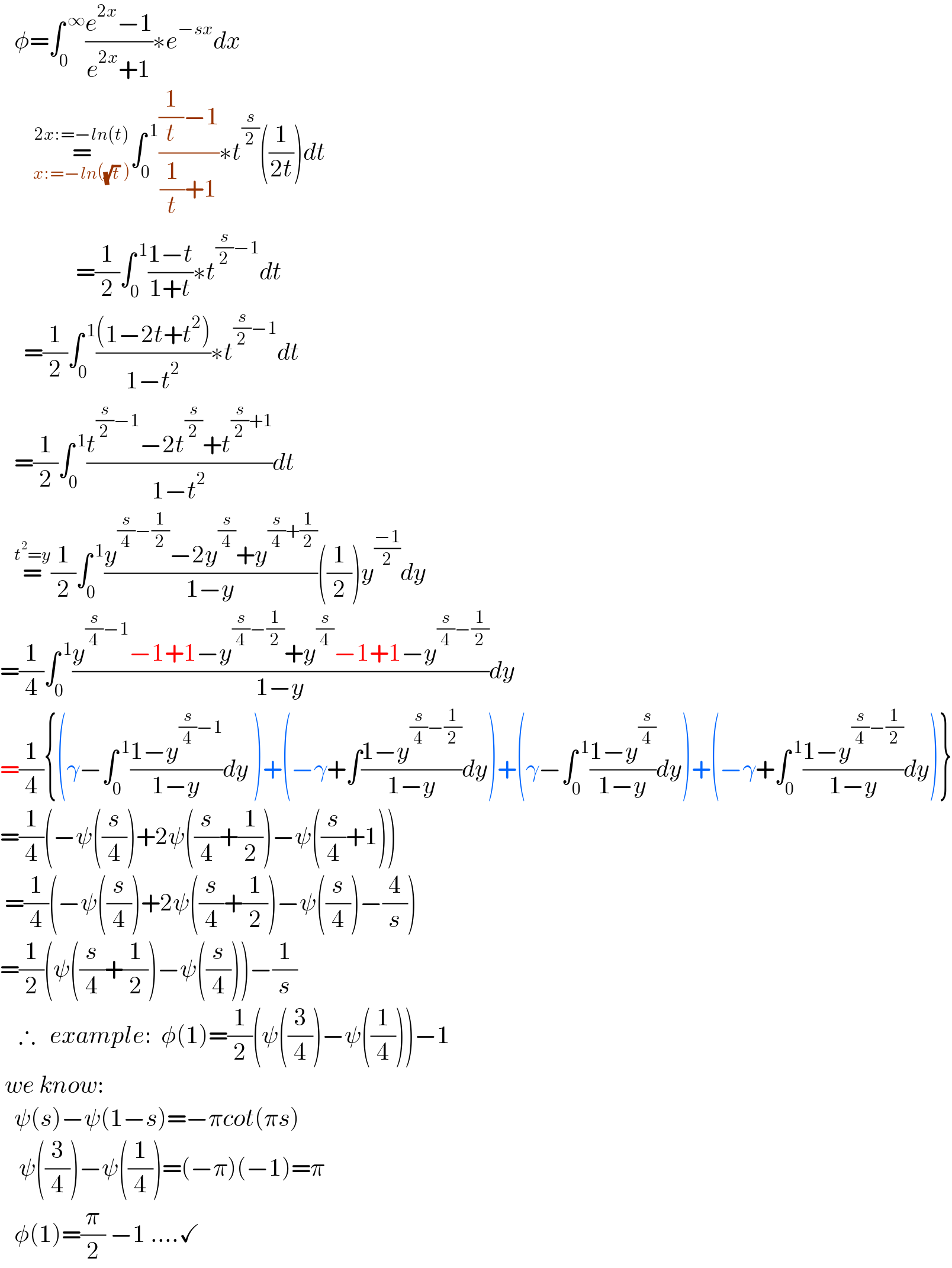
φ=∫_0 ^( ∞) ((e^(2x) −1)/(e^(2x) +1))∗e^(−sx) dx =_(x:=−ln((√t) )) ^(2x:=−ln(t)) ∫_0 ^( 1) (((1/t)−1)/((1/t)+1))∗t^(s/2) ((1/(2t)))dt =(1/2)∫_0 ^( 1) ((1−t)/(1+t))∗t^((s/2)−1) dt =(1/2)∫_0 ^( 1) (((1−2t+t^2 ))/(1−t^2 ))∗t^((s/2)−1) dt =(1/2)∫_0 ^( 1) ((t^((s/2)−1) −2t^(s/2) +t^((s/2)+1) )/(1−t^2 ))dt =^(t^2 =y) (1/2)∫_0 ^( 1) ((y^((s/4)−(1/2)) −2y^(s/4) +y^((s/4)+(1/2)) )/(1−y))((1/2))y^((−1)/2) dy =(1/4)∫_0 ^( 1) ((y^((s/4)−1) −1+1−y^((s/4)−(1/2)) +y^(s/4) −1+1−y^((s/4)−(1/2)) )/(1−y))dy =(1/4){(γ−∫_0 ^( 1) ((1−y^((s/4)−1) )/(1−y))dy )+(−γ+∫((1−y^((s/4)−(1/2)) )/(1−y))dy)+(γ−∫_0 ^( 1) ((1−y^(s/4) )/(1−y))dy)+(−γ+∫_0 ^( 1) ((1−y^((s/4)−(1/2)) )/(1−y))dy)} =(1/4)(−ψ((s/4))+2ψ((s/4)+(1/2))−ψ((s/4)+1)) =(1/4)(−ψ((s/4))+2ψ((s/4)+(1/2))−ψ((s/4))−(4/s)) =(1/2)(ψ((s/4)+(1/2))−ψ((s/4)))−(1/s) ∴ example: φ(1)=(1/2)(ψ((3/4))−ψ((1/4)))−1 we know: ψ(s)−ψ(1−s)=−πcot(πs) ψ((3/4))−ψ((1/4))=(−π)(−1)=π φ(1)=(π/2) −1 ....✓

$$\:\:\:\phi=\int_{\mathrm{0}} ^{\:\infty} \frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{{e}^{\mathrm{2}{x}} +\mathrm{1}}\ast{e}^{−{sx}} {dx} \\ $$ $$\:\:\:\:\:\:\:\underset{{x}:=−{ln}\left(\sqrt{{t}}\:\right)} {\overset{\mathrm{2}{x}:=−{ln}\left({t}\right)} {=}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\frac{\mathrm{1}}{{t}}−\mathrm{1}}{\frac{\mathrm{1}}{{t}}+\mathrm{1}}\ast{t}^{\frac{{s}}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{2}{t}}\right){dt} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\ast{t}^{\frac{{s}}{\mathrm{2}}−\mathrm{1}} {dt} \\ $$ $$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{2}{t}+{t}^{\mathrm{2}} \right)}{\mathrm{1}−{t}^{\mathrm{2}} }\ast{t}^{\frac{{s}}{\mathrm{2}}−\mathrm{1}} {dt} \\ $$ $$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{t}^{\frac{{s}}{\mathrm{2}}−\mathrm{1}} −\mathrm{2}{t}^{\frac{{s}}{\mathrm{2}}} +{t}^{\frac{{s}}{\mathrm{2}}+\mathrm{1}} }{\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$ $$\:\:\:\overset{{t}^{\mathrm{2}} ={y}} {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{y}^{\frac{{s}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{2}{y}^{\frac{{s}}{\mathrm{4}}} +{y}^{\frac{{s}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}−{y}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){y}^{\frac{−\mathrm{1}}{\mathrm{2}}} {dy} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{y}^{\frac{{s}}{\mathrm{4}}−\mathrm{1}} −\mathrm{1}+\mathrm{1}−{y}^{\frac{{s}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}} +{y}^{\frac{{s}}{\mathrm{4}}} −\mathrm{1}+\mathrm{1}−{y}^{\frac{{s}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}−{y}}{dy} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\left(\gamma−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{y}^{\frac{{s}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}−{y}}{dy}\:\right)+\left(−\gamma+\int\frac{\mathrm{1}−{y}^{\frac{{s}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}−{y}}{dy}\right)+\left(\gamma−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{y}^{\frac{{s}}{\mathrm{4}}} }{\mathrm{1}−{y}}{dy}\right)+\left(−\gamma+\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{y}^{\frac{{s}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}−{y}}{dy}\right)\right\} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{4}}\left(−\psi\left(\frac{{s}}{\mathrm{4}}\right)+\mathrm{2}\psi\left(\frac{{s}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{{s}}{\mathrm{4}}+\mathrm{1}\right)\right) \\ $$ $$\:=\frac{\mathrm{1}}{\mathrm{4}}\left(−\psi\left(\frac{{s}}{\mathrm{4}}\right)+\mathrm{2}\psi\left(\frac{{s}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{{s}}{\mathrm{4}}\right)−\frac{\mathrm{4}}{{s}}\right) \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}\left(\psi\left(\frac{{s}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{{s}}{\mathrm{4}}\right)\right)−\frac{\mathrm{1}}{{s}} \\ $$ $$\:\:\:\:\therefore\:\:\:{example}:\:\:\phi\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right)−\mathrm{1} \\ $$ $$\:{we}\:{know}: \\ $$ $$\:\:\:\psi\left({s}\right)−\psi\left(\mathrm{1}−{s}\right)=−\pi{cot}\left(\pi{s}\right) \\ $$ $$\:\:\:\:\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\left(−\pi\right)\left(−\mathrm{1}\right)=\pi \\ $$ $$\:\:\:\phi\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{2}}\:−\mathrm{1}\:....\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com