
Question Number 130383 by MrHusseinElmasry last updated on 25/Jan/21
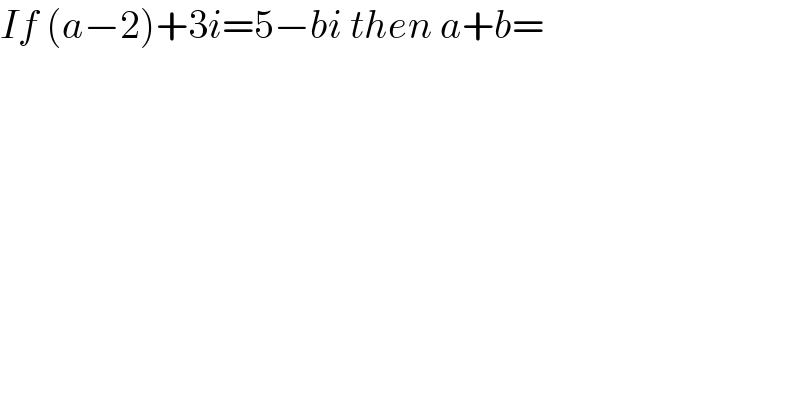
$${If}\:\left({a}−\mathrm{2}\right)+\mathrm{3}{i}=\mathrm{5}−{bi}\:{then}\:{a}+{b}= \\ $$
Answered by mathmax by abdo last updated on 25/Jan/21
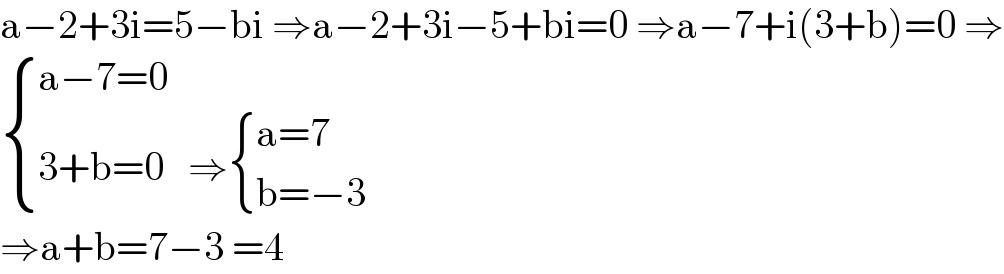
$$\mathrm{a}−\mathrm{2}+\mathrm{3i}=\mathrm{5}−\mathrm{bi}\:\Rightarrow\mathrm{a}−\mathrm{2}+\mathrm{3i}−\mathrm{5}+\mathrm{bi}=\mathrm{0}\:\Rightarrow\mathrm{a}−\mathrm{7}+\mathrm{i}\left(\mathrm{3}+\mathrm{b}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\begin{cases}{\mathrm{a}−\mathrm{7}=\mathrm{0}}\\{\mathrm{3}+\mathrm{b}=\mathrm{0}\:\:\:\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{7}}\\{\mathrm{b}=−\mathrm{3}\:}\end{cases}}\end{cases} \\ $$$$\Rightarrow\mathrm{a}+\mathrm{b}=\mathrm{7}−\mathrm{3}\:=\mathrm{4} \\ $$
Commented by mathmax by abdo last updated on 25/Jan/21
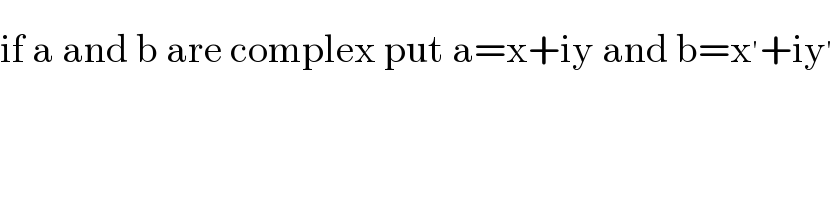
$$\mathrm{if}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b}\:\mathrm{are}\:\mathrm{complex}\:\mathrm{put}\:\mathrm{a}=\mathrm{x}+\mathrm{iy}\:\mathrm{and}\:\mathrm{b}=\mathrm{x}^{'} +\mathrm{iy}^{'} \\ $$
