
Question Number 130350 by ajfour last updated on 24/Jan/21
Commented by ajfour last updated on 24/Jan/21

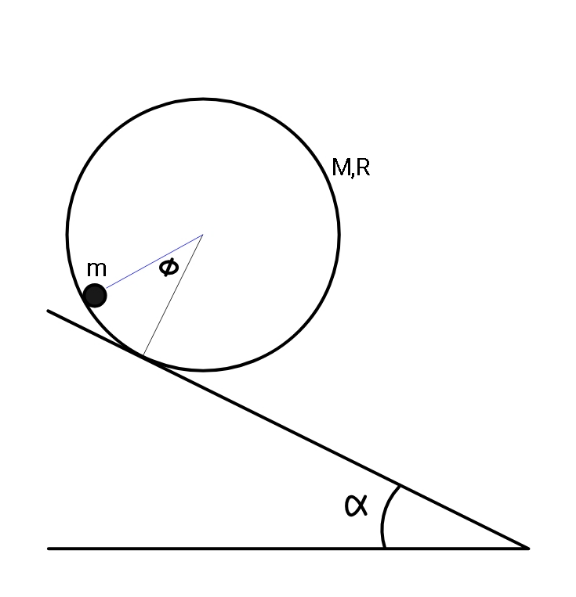
$${A}\:{hollow}\:{cylinder}\:\left({radius}\:{R},\right. \\ $$$$\left.{mass}\:{M}\right)\:{rolling}\:{down}\:{a}\:{long} \\ $$$${incline},\:{has}\:{a}\:{small}\:{ball}\:{at} \\ $$$${an}\:{angular}\:{position}\:\boldsymbol{\phi}. \\ $$$${Determine}\:\boldsymbol{\phi}\:{in}\:{terms}\:{of} \\ $$$$\alpha,\:{g},\:{m},\:{M},\:{and}\:{R}. \\ $$
Answered by mr W last updated on 25/Jan/21
Commented by mr W last updated on 25/Jan/21
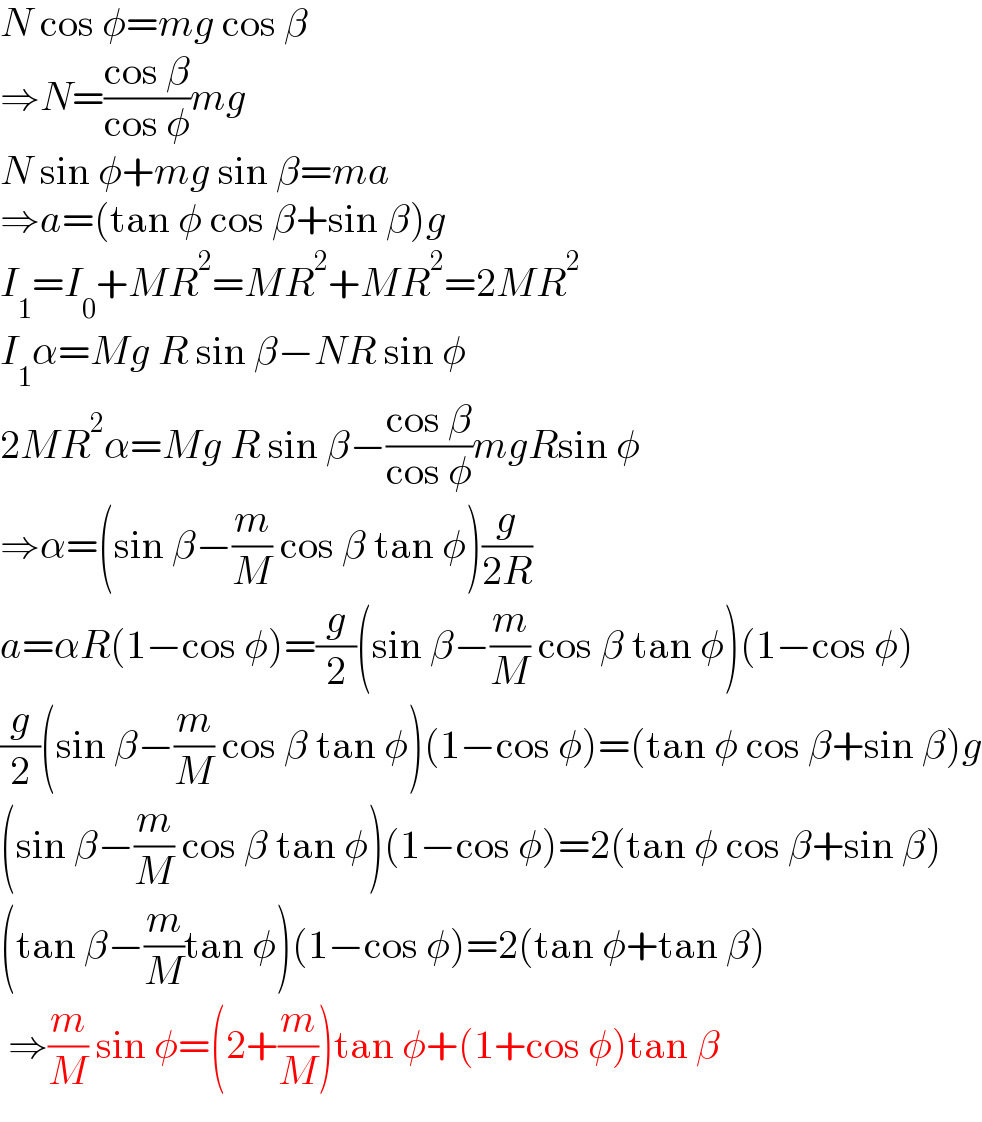
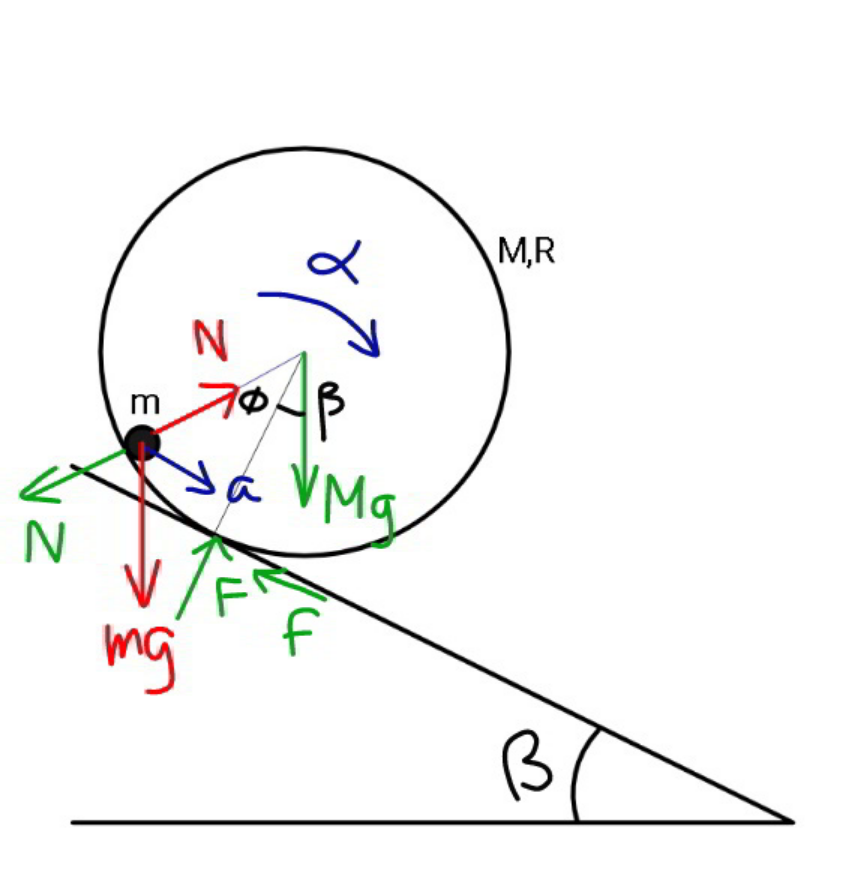
$${N}\:\mathrm{cos}\:\phi={mg}\:\mathrm{cos}\:\beta \\ $$$$\Rightarrow{N}=\frac{\mathrm{cos}\:\beta}{\mathrm{cos}\:\phi}{mg} \\ $$$${N}\:\mathrm{sin}\:\phi+{mg}\:\mathrm{sin}\:\beta={ma} \\ $$$$\Rightarrow{a}=\left(\mathrm{tan}\:\phi\:\mathrm{cos}\:\beta+\mathrm{sin}\:\beta\right){g} \\ $$$${I}_{\mathrm{1}} ={I}_{\mathrm{0}} +{MR}^{\mathrm{2}} ={MR}^{\mathrm{2}} +{MR}^{\mathrm{2}} =\mathrm{2}{MR}^{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} \alpha={Mg}\:{R}\:\mathrm{sin}\:\beta−{NR}\:\mathrm{sin}\:\phi \\ $$$$\mathrm{2}{MR}^{\mathrm{2}} \alpha={Mg}\:{R}\:\mathrm{sin}\:\beta−\frac{\mathrm{cos}\:\beta}{\mathrm{cos}\:\phi}{mgR}\mathrm{sin}\:\phi \\ $$$$\Rightarrow\alpha=\left(\mathrm{sin}\:\beta−\frac{{m}}{{M}}\:\mathrm{cos}\:\beta\:\mathrm{tan}\:\phi\right)\frac{{g}}{\mathrm{2}{R}} \\ $$$${a}=\alpha{R}\left(\mathrm{1}−\mathrm{cos}\:\phi\right)=\frac{{g}}{\mathrm{2}}\left(\mathrm{sin}\:\beta−\frac{{m}}{{M}}\:\mathrm{cos}\:\beta\:\mathrm{tan}\:\phi\right)\left(\mathrm{1}−\mathrm{cos}\:\phi\right) \\ $$$$\frac{{g}}{\mathrm{2}}\left(\mathrm{sin}\:\beta−\frac{{m}}{{M}}\:\mathrm{cos}\:\beta\:\mathrm{tan}\:\phi\right)\left(\mathrm{1}−\mathrm{cos}\:\phi\right)=\left(\mathrm{tan}\:\phi\:\mathrm{cos}\:\beta+\mathrm{sin}\:\beta\right){g} \\ $$$$\left(\mathrm{sin}\:\beta−\frac{{m}}{{M}}\:\mathrm{cos}\:\beta\:\mathrm{tan}\:\phi\right)\left(\mathrm{1}−\mathrm{cos}\:\phi\right)=\mathrm{2}\left(\mathrm{tan}\:\phi\:\mathrm{cos}\:\beta+\mathrm{sin}\:\beta\right) \\ $$$$\left(\mathrm{tan}\:\beta−\frac{{m}}{{M}}\mathrm{tan}\:\phi\right)\left(\mathrm{1}−\mathrm{cos}\:\phi\right)=\mathrm{2}\left(\mathrm{tan}\:\phi+\mathrm{tan}\:\beta\right) \\ $$$$\:\Rightarrow\frac{{m}}{{M}}\:\mathrm{sin}\:\phi=\left(\mathrm{2}+\frac{{m}}{{M}}\right)\mathrm{tan}\:\phi+\left(\mathrm{1}+\mathrm{cos}\:\phi\right)\mathrm{tan}\:\beta \\ $$
Commented by ajfour last updated on 26/Jan/21

$${Sir}\:\:{i}\:{think}, \\ $$$$\:\:{a}=\alpha{R}\:\: \\ $$
Commented by mr W last updated on 26/Jan/21

$${you}\:{are}\:{right}\:{sir}! \\ $$
Commented by ajfour last updated on 26/Jan/21
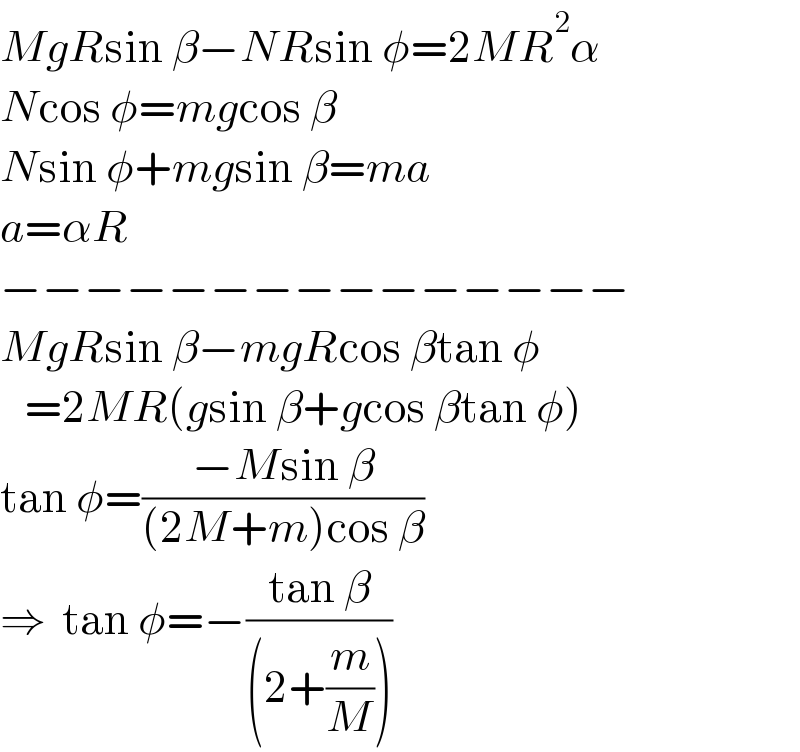
$${MgR}\mathrm{sin}\:\beta−{NR}\mathrm{sin}\:\phi=\mathrm{2}{MR}^{\mathrm{2}} \alpha \\ $$$${N}\mathrm{cos}\:\phi={mg}\mathrm{cos}\:\beta \\ $$$${N}\mathrm{sin}\:\phi+{mg}\mathrm{sin}\:\beta={ma} \\ $$$${a}=\alpha{R} \\ $$$$−−−−−−−−−−−−−−− \\ $$$${MgR}\mathrm{sin}\:\beta−{mgR}\mathrm{cos}\:\beta\mathrm{tan}\:\phi \\ $$$$\:\:\:=\mathrm{2}{MR}\left({g}\mathrm{sin}\:\beta+{g}\mathrm{cos}\:\beta\mathrm{tan}\:\phi\right) \\ $$$$\mathrm{tan}\:\phi=\frac{−{M}\mathrm{sin}\:\beta}{\left(\mathrm{2}{M}+{m}\right)\mathrm{cos}\:\beta} \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\phi=−\frac{\mathrm{tan}\:\beta}{\left(\mathrm{2}+\frac{{m}}{{M}}\right)} \\ $$
Commented by ajfour last updated on 26/Jan/21
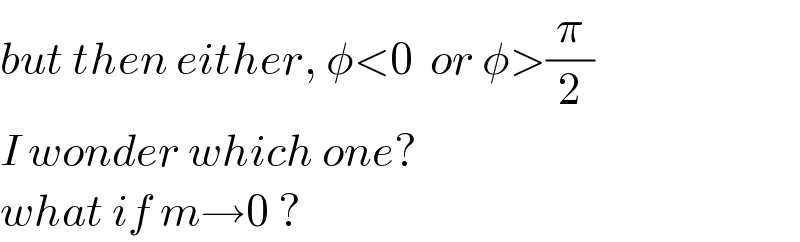
$${but}\:{then}\:{either},\:\phi<\mathrm{0}\:\:{or}\:\phi>\frac{\pi}{\mathrm{2}} \\ $$$${I}\:{wonder}\:{which}\:{one}? \\ $$$${what}\:{if}\:{m}\rightarrow\mathrm{0}\:? \\ $$
Commented by mr W last updated on 26/Jan/21
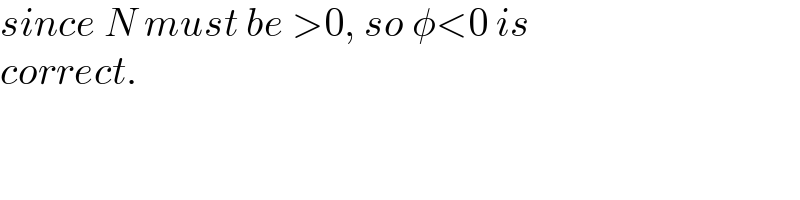
$${since}\:{N}\:{must}\:{be}\:>\mathrm{0},\:{so}\:\phi<\mathrm{0}\:{is} \\ $$$${correct}. \\ $$
Commented by ajfour last updated on 26/Jan/21
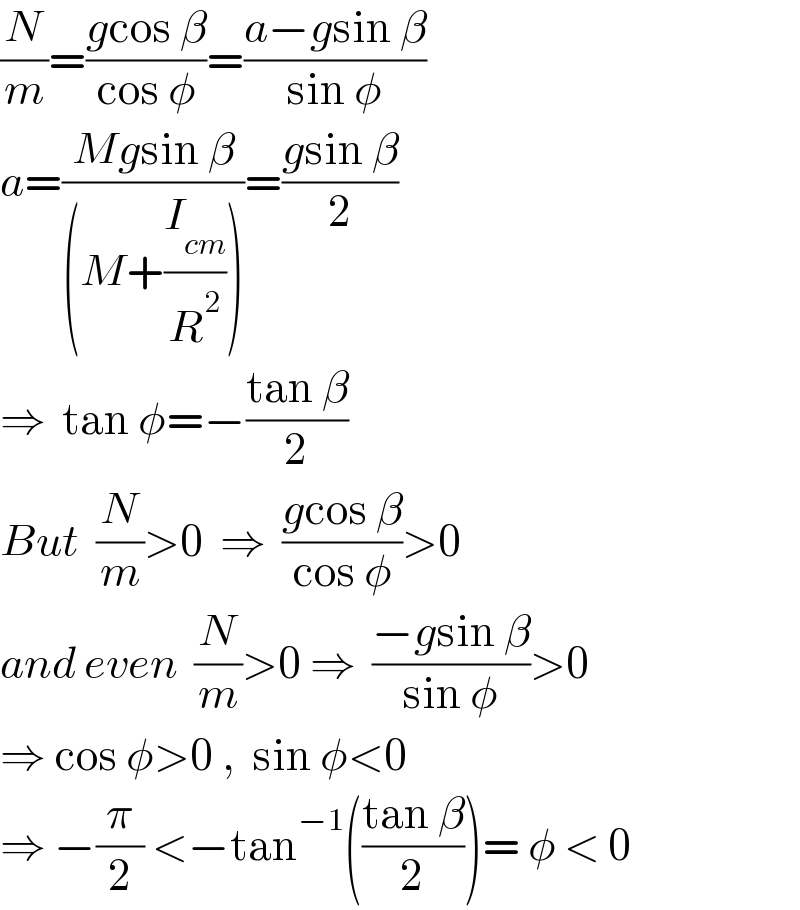
$$\frac{{N}}{{m}}=\frac{{g}\mathrm{cos}\:\beta}{\mathrm{cos}\:\phi}=\frac{{a}−{g}\mathrm{sin}\:\beta}{\mathrm{sin}\:\phi} \\ $$$${a}=\frac{{Mg}\mathrm{sin}\:\beta}{\left({M}+\frac{{I}_{{cm}} }{{R}^{\mathrm{2}} }\right)}=\frac{{g}\mathrm{sin}\:\beta}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\phi=−\frac{\mathrm{tan}\:\beta}{\mathrm{2}} \\ $$$${But}\:\:\frac{{N}}{{m}}>\mathrm{0}\:\:\Rightarrow\:\:\frac{{g}\mathrm{cos}\:\beta}{\mathrm{cos}\:\phi}>\mathrm{0} \\ $$$${and}\:{even}\:\:\frac{{N}}{{m}}>\mathrm{0}\:\Rightarrow\:\:\frac{−{g}\mathrm{sin}\:\beta}{\mathrm{sin}\:\phi}>\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{cos}\:\phi>\mathrm{0}\:,\:\:\mathrm{sin}\:\phi<\mathrm{0} \\ $$$$\Rightarrow\:−\frac{\pi}{\mathrm{2}}\:<−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\beta}{\mathrm{2}}\right)=\:\phi\:<\:\mathrm{0} \\ $$
Answered by mr W last updated on 26/Jan/21
Commented by mr W last updated on 26/Jan/21
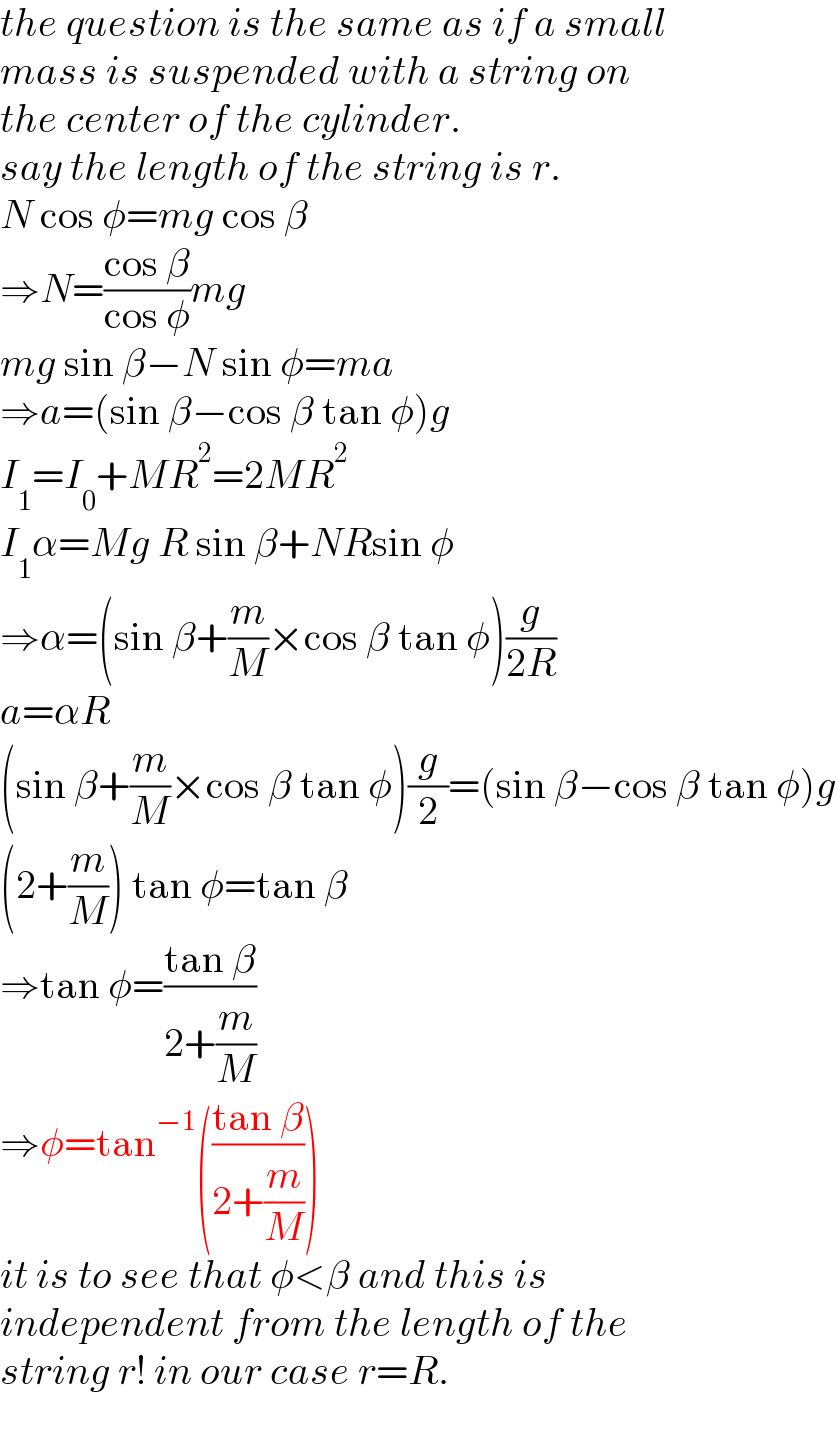
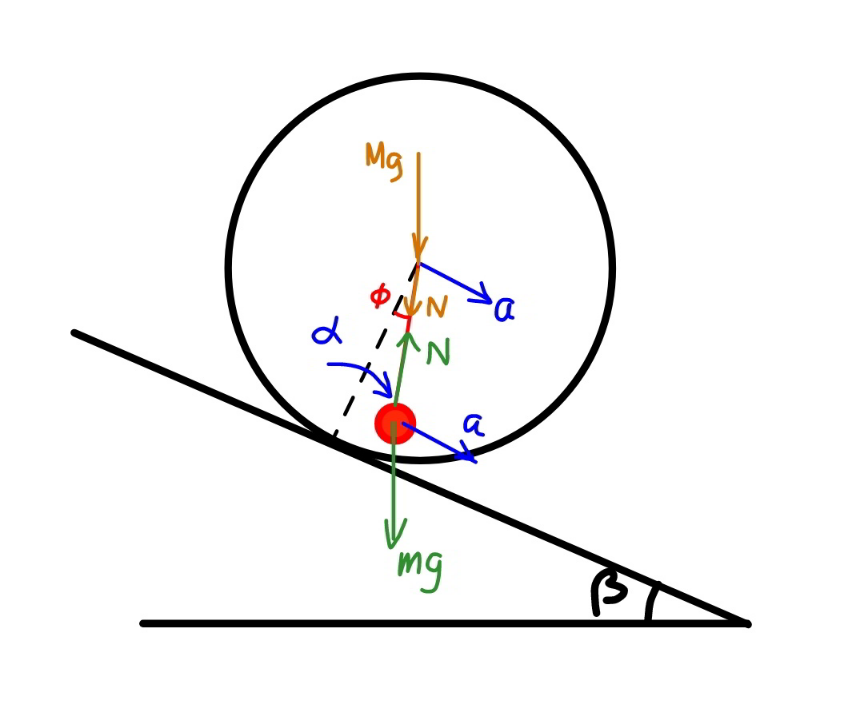
$${the}\:{question}\:{is}\:{the}\:{same}\:{as}\:{if}\:{a}\:{small} \\ $$$${mass}\:{is}\:{suspended}\:{with}\:{a}\:{string}\:{on} \\ $$$${the}\:{center}\:{of}\:{the}\:{cylinder}. \\ $$$${say}\:{the}\:{length}\:{of}\:{the}\:{string}\:{is}\:{r}. \\ $$$${N}\:\mathrm{cos}\:\phi={mg}\:\mathrm{cos}\:\beta \\ $$$$\Rightarrow{N}=\frac{\mathrm{cos}\:\beta}{\mathrm{cos}\:\phi}{mg} \\ $$$${mg}\:\mathrm{sin}\:\beta−{N}\:\mathrm{sin}\:\phi={ma} \\ $$$$\Rightarrow{a}=\left(\mathrm{sin}\:\beta−\mathrm{cos}\:\beta\:\mathrm{tan}\:\phi\right){g} \\ $$$${I}_{\mathrm{1}} ={I}_{\mathrm{0}} +{MR}^{\mathrm{2}} =\mathrm{2}{MR}^{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} \alpha={Mg}\:{R}\:\mathrm{sin}\:\beta+{NR}\mathrm{sin}\:\phi \\ $$$$\Rightarrow\alpha=\left(\mathrm{sin}\:\beta+\frac{{m}}{{M}}×\mathrm{cos}\:\beta\:\mathrm{tan}\:\phi\right)\frac{{g}}{\mathrm{2}{R}} \\ $$$${a}=\alpha{R} \\ $$$$\left(\mathrm{sin}\:\beta+\frac{{m}}{{M}}×\mathrm{cos}\:\beta\:\mathrm{tan}\:\phi\right)\frac{{g}}{\mathrm{2}}=\left(\mathrm{sin}\:\beta−\mathrm{cos}\:\beta\:\mathrm{tan}\:\phi\right){g} \\ $$$$\left(\mathrm{2}+\frac{{m}}{{M}}\right)\:\mathrm{tan}\:\phi=\mathrm{tan}\:\beta \\ $$$$\Rightarrow\mathrm{tan}\:\phi=\frac{\mathrm{tan}\:\beta}{\mathrm{2}+\frac{{m}}{{M}}} \\ $$$$\Rightarrow\phi=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\beta}{\mathrm{2}+\frac{{m}}{{M}}}\right) \\ $$$${it}\:{is}\:{to}\:{see}\:{that}\:\phi<\beta\:{and}\:{this}\:{is} \\ $$$${independent}\:{from}\:{the}\:{length}\:{of}\:{the} \\ $$$${string}\:{r}!\:{in}\:{our}\:{case}\:{r}={R}. \\ $$
Answered by mr W last updated on 27/Jan/21
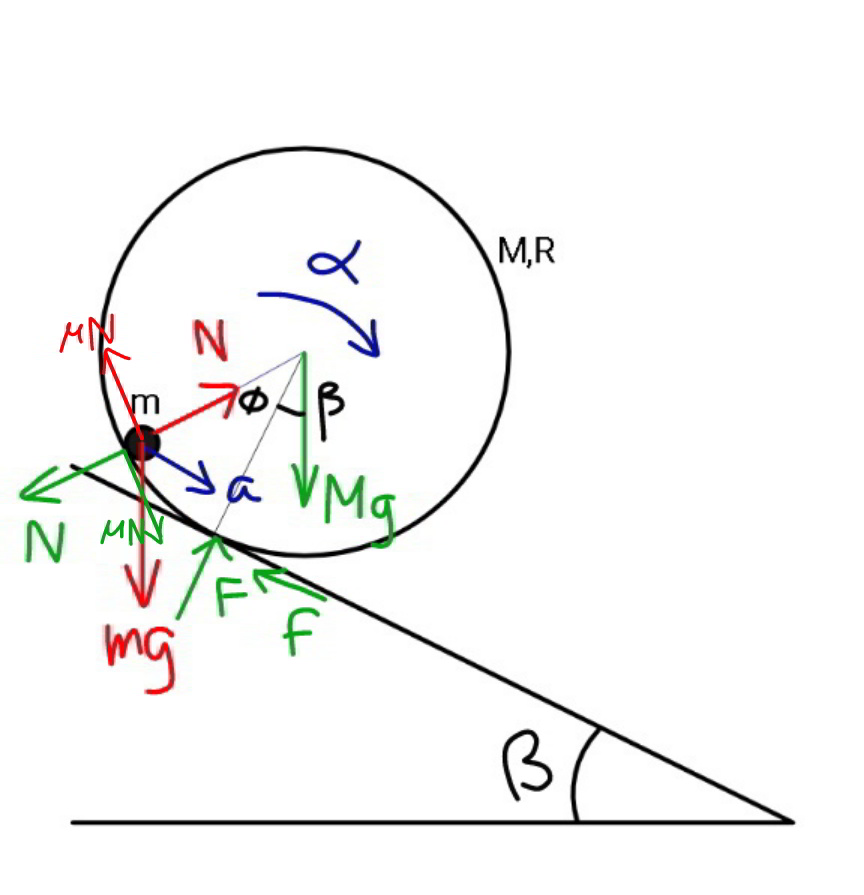
Commented by mr W last updated on 28/Jan/21
![friction coefficient between ball and cylinder =μ N cos φ+μN sin φ=mg cos β ⇒N=((cos β)/(cos φ+μ sin φ))mg ma=N sin φ−μN cos φ+mg sin β ⇒a=[((cos β (tan φ−μ))/(1+μ tan φ))+sin β]g 2MR^2 α=MgR sin β−NR sin φ−μNR(1−cos φ) 2Rα={sin β−(m/M)×((cos β(μ+sin φ−μ cos φ))/(cos φ+μ sin φ))}g 2a={sin β−(m/M)×((cos β(μ+sin φ−μ cos φ))/(cos φ+μ sin φ))}g ((2(tan φ−μ))/(1+μ tan φ))+2tan β=tan β−(m/M)×((μ+sin φ−μ cos φ)/(cos φ+μ sin φ)) ⇒((((mμ)/(Mcos φ))+(2+(m/M))(tan φ−μ))/(1+μ tan φ))=−tan β let λ=(m/M), η=tan β ((λμ+(2+λ)(sin φ−μ cos φ))/(cos φ+μ sin φ))=−η (2+λ+μη)sin φ−(2μ+λμ−η) cos φ=−λμ let δ=tan^(−1) ((2μ+λμ−η)/(2+λ+μη)) sin (φ−δ)=−((λμ)/( (√((2+λ+μη)^2 +(2μ+λμ−η)^2 )))) φ=tan^(−1) ((2μ+λμ−η)/(2+λ+μη))−sin^(−1) ((λμ)/( (√((2+λ+μη)^2 +(2μ+λμ−η)^2 )))) ⇒φ=tan^(−1) (((2+(m/M))μ−tan β)/(2+(m/M)+μ tan β))−sin^(−1) (((μm)/M)/( (√((1+μ^2 ) [tan^2 β+(2+(m/M))^2 ])))) examples: β=30°, (m/M)=0.2, μ=1 ⇒φ=26.7306° β=30°, (m/M)=0.2, μ=0.5 ⇒φ=9.6067° β=30°, (m/M)=0.2, μ=((√3)/6)=0.289 ⇒φ=0 β=30°, (m/M)=0.2, μ=0 ⇒φ=−14.7047°](Q130663.png)
$${friction}\:{coefficient}\:{between}\:{ball} \\ $$$${and}\:{cylinder}\:=\mu \\ $$$${N}\:\mathrm{cos}\:\phi+\mu{N}\:\mathrm{sin}\:\phi={mg}\:\mathrm{cos}\:\beta \\ $$$$\Rightarrow{N}=\frac{\mathrm{cos}\:\beta}{\mathrm{cos}\:\phi+\mu\:\mathrm{sin}\:\phi}{mg} \\ $$$${ma}={N}\:\mathrm{sin}\:\phi−\mu{N}\:\mathrm{cos}\:\phi+{mg}\:\mathrm{sin}\:\beta \\ $$$$\Rightarrow{a}=\left[\frac{\mathrm{cos}\:\beta\:\left(\mathrm{tan}\:\phi−\mu\right)}{\mathrm{1}+\mu\:\mathrm{tan}\:\phi}+\mathrm{sin}\:\beta\right]{g} \\ $$$$\mathrm{2}{MR}^{\mathrm{2}} \alpha={MgR}\:\mathrm{sin}\:\beta−{NR}\:\mathrm{sin}\:\phi−\mu{NR}\left(\mathrm{1}−\mathrm{cos}\:\phi\right) \\ $$$$\mathrm{2}{R}\alpha=\left\{\mathrm{sin}\:\beta−\frac{{m}}{{M}}×\frac{\mathrm{cos}\:\beta\left(\mu+\mathrm{sin}\:\phi−\mu\:\mathrm{cos}\:\phi\right)}{\mathrm{cos}\:\phi+\mu\:\mathrm{sin}\:\phi}\right\}{g} \\ $$$$\mathrm{2}{a}=\left\{\mathrm{sin}\:\beta−\frac{{m}}{{M}}×\frac{\mathrm{cos}\:\beta\left(\mu+\mathrm{sin}\:\phi−\mu\:\mathrm{cos}\:\phi\right)}{\mathrm{cos}\:\phi+\mu\:\mathrm{sin}\:\phi}\right\}{g} \\ $$$$\frac{\mathrm{2}\left(\mathrm{tan}\:\phi−\mu\right)}{\mathrm{1}+\mu\:\mathrm{tan}\:\phi}+\mathrm{2tan}\:\beta=\mathrm{tan}\:\beta−\frac{{m}}{{M}}×\frac{\mu+\mathrm{sin}\:\phi−\mu\:\mathrm{cos}\:\phi}{\mathrm{cos}\:\phi+\mu\:\mathrm{sin}\:\phi} \\ $$$$\Rightarrow\frac{\frac{{m}\mu}{{M}\mathrm{cos}\:\phi}+\left(\mathrm{2}+\frac{{m}}{{M}}\right)\left(\mathrm{tan}\:\phi−\mu\right)}{\mathrm{1}+\mu\:\mathrm{tan}\:\phi}=−\mathrm{tan}\:\beta \\ $$$${let}\:\lambda=\frac{{m}}{{M}},\:\eta=\mathrm{tan}\:\beta \\ $$$$\frac{\lambda\mu+\left(\mathrm{2}+\lambda\right)\left(\mathrm{sin}\:\phi−\mu\:\mathrm{cos}\:\phi\right)}{\mathrm{cos}\:\phi+\mu\:\mathrm{sin}\:\phi}=−\eta \\ $$$$\left(\mathrm{2}+\lambda+\mu\eta\right)\mathrm{sin}\:\phi−\left(\mathrm{2}\mu+\lambda\mu−\eta\right)\:\mathrm{cos}\:\phi=−\lambda\mu \\ $$$${let}\:\delta=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}\mu+\lambda\mu−\eta}{\mathrm{2}+\lambda+\mu\eta} \\ $$$$\mathrm{sin}\:\left(\phi−\delta\right)=−\frac{\lambda\mu}{\:\sqrt{\left(\mathrm{2}+\lambda+\mu\eta\right)^{\mathrm{2}} +\left(\mathrm{2}\mu+\lambda\mu−\eta\right)^{\mathrm{2}} }} \\ $$$$\phi=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}\mu+\lambda\mu−\eta}{\mathrm{2}+\lambda+\mu\eta}−\mathrm{sin}^{−\mathrm{1}} \frac{\lambda\mu}{\:\sqrt{\left(\mathrm{2}+\lambda+\mu\eta\right)^{\mathrm{2}} +\left(\mathrm{2}\mu+\lambda\mu−\eta\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\phi=\mathrm{tan}^{−\mathrm{1}} \frac{\left(\mathrm{2}+\frac{{m}}{{M}}\right)\mu−\mathrm{tan}\:\beta}{\mathrm{2}+\frac{{m}}{{M}}+\mu\:\mathrm{tan}\:\beta}−\mathrm{sin}^{−\mathrm{1}} \frac{\frac{\mu{m}}{{M}}}{\:\sqrt{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\:\left[\mathrm{tan}^{\mathrm{2}} \:\beta+\left(\mathrm{2}+\frac{{m}}{{M}}\right)^{\mathrm{2}} \right]}} \\ $$$$ \\ $$$${examples}: \\ $$$$\beta=\mathrm{30}°,\:\frac{{m}}{{M}}=\mathrm{0}.\mathrm{2},\:\mu=\mathrm{1}\:\Rightarrow\phi=\mathrm{26}.\mathrm{7306}° \\ $$$$\beta=\mathrm{30}°,\:\frac{{m}}{{M}}=\mathrm{0}.\mathrm{2},\:\mu=\mathrm{0}.\mathrm{5}\:\Rightarrow\phi=\mathrm{9}.\mathrm{6067}° \\ $$$$\beta=\mathrm{30}°,\:\frac{{m}}{{M}}=\mathrm{0}.\mathrm{2},\:\mu=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}=\mathrm{0}.\mathrm{289}\:\Rightarrow\phi=\mathrm{0} \\ $$$$\beta=\mathrm{30}°,\:\frac{{m}}{{M}}=\mathrm{0}.\mathrm{2},\:\mu=\mathrm{0}\:\Rightarrow\phi=−\mathrm{14}.\mathrm{7047}° \\ $$
Commented by ajfour last updated on 28/Jan/21

$${Great}\:{generalisation},\:{Sir}. \\ $$$${Thanks}\:{for}\:{the}\:{analysis}. \\ $$
