
Question Number 130326 by rs4089 last updated on 24/Jan/21
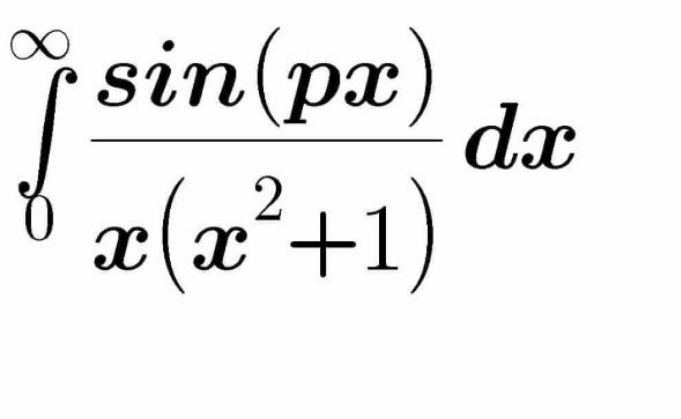
Answered by Lordose last updated on 24/Jan/21
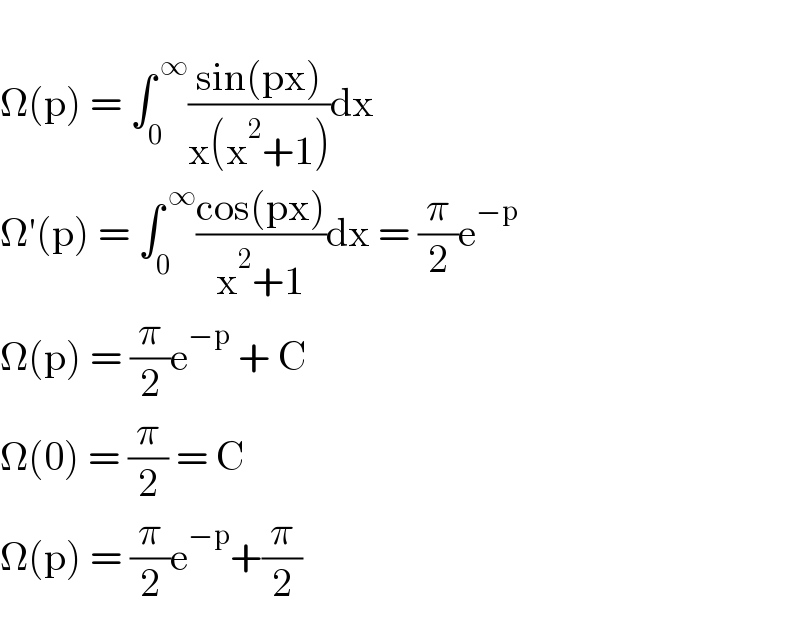
$$ \\ $$$$\Omega\left(\mathrm{p}\right)\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{sin}\left(\mathrm{px}\right)}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dx} \\ $$$$\Omega'\left(\mathrm{p}\right)\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{cos}\left(\mathrm{px}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:=\:\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{p}} \\ $$$$\Omega\left(\mathrm{p}\right)\:=\:\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{p}} \:+\:\mathrm{C} \\ $$$$\Omega\left(\mathrm{0}\right)\:=\:\frac{\pi}{\mathrm{2}}\:=\:\mathrm{C} \\ $$$$\Omega\left(\mathrm{p}\right)\:=\:\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{p}} +\frac{\pi}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 24/Jan/21
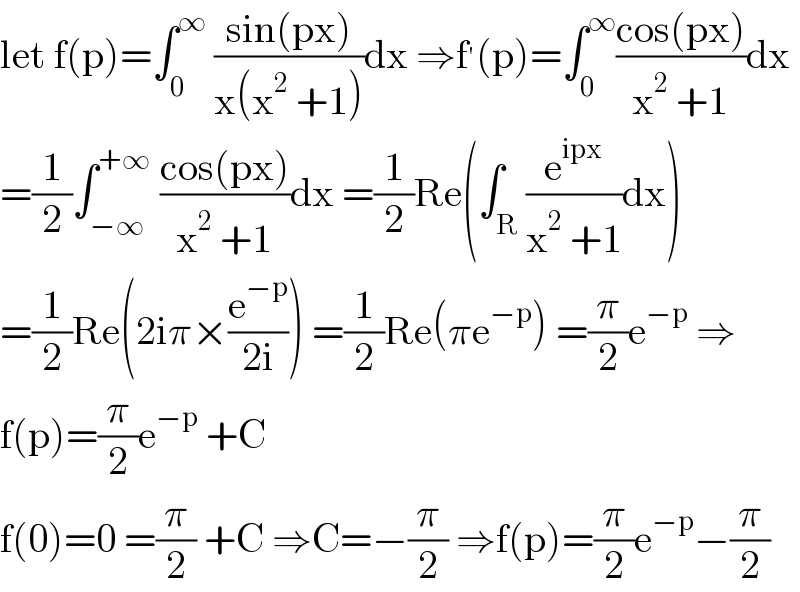
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{p}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{px}\right)}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{p}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cos}\left(\mathrm{px}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{px}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\int_{\mathrm{R}} \frac{\mathrm{e}^{\mathrm{ipx}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\mathrm{2i}\pi×\frac{\mathrm{e}^{−\mathrm{p}} }{\mathrm{2i}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\pi\mathrm{e}^{−\mathrm{p}} \right)\:=\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{p}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{p}\right)=\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{p}} \:+\mathrm{C} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}\:=\frac{\pi}{\mathrm{2}}\:+\mathrm{C}\:\Rightarrow\mathrm{C}=−\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{f}\left(\mathrm{p}\right)=\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{p}} −\frac{\pi}{\mathrm{2}} \\ $$
