
Question Number 130257 by pete last updated on 23/Jan/21
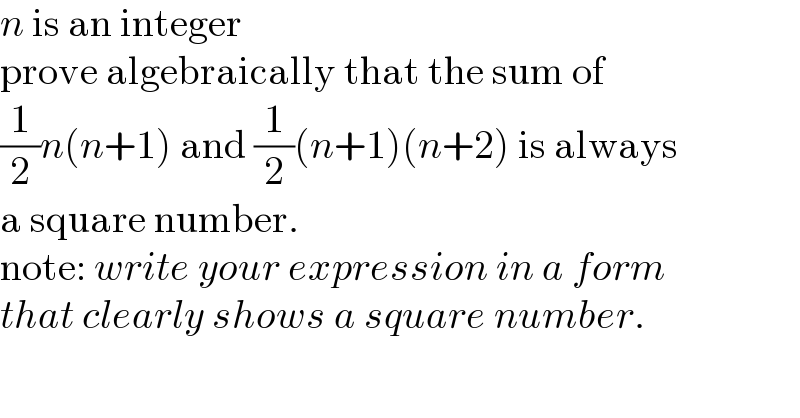
$${n}\:\mathrm{is}\:\mathrm{an}\:\mathrm{integer} \\ $$$$\mathrm{prove}\:\mathrm{algebraically}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{n}\left({n}+\mathrm{1}\right)\:\mathrm{and}\:\frac{\mathrm{1}}{\mathrm{2}}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\:\mathrm{is}\:\mathrm{always} \\ $$$$\mathrm{a}\:\mathrm{square}\:\mathrm{number}. \\ $$$$\mathrm{note}:\:{write}\:{your}\:{expression}\:{in}\:{a}\:{form} \\ $$$${that}\:{clearly}\:{shows}\:{a}\:{square}\:{number}. \\ $$
Commented by Dwaipayan Shikari last updated on 23/Jan/21
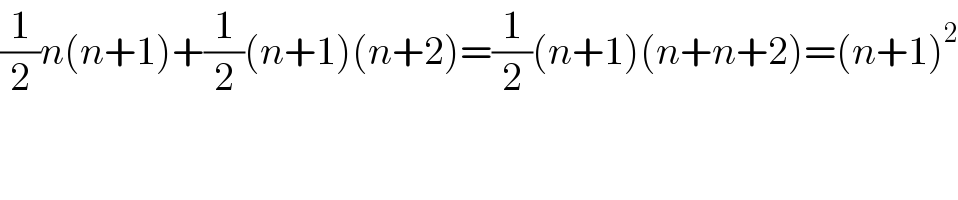
$$\frac{\mathrm{1}}{\mathrm{2}}{n}\left({n}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({n}+\mathrm{1}\right)\left({n}+{n}+\mathrm{2}\right)=\left({n}+\mathrm{1}\right)^{\mathrm{2}} \\ $$
Commented by pete last updated on 23/Jan/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{very}\:\mathrm{much} \\ $$
