
Question Number 130186 by mohammad17 last updated on 23/Jan/21
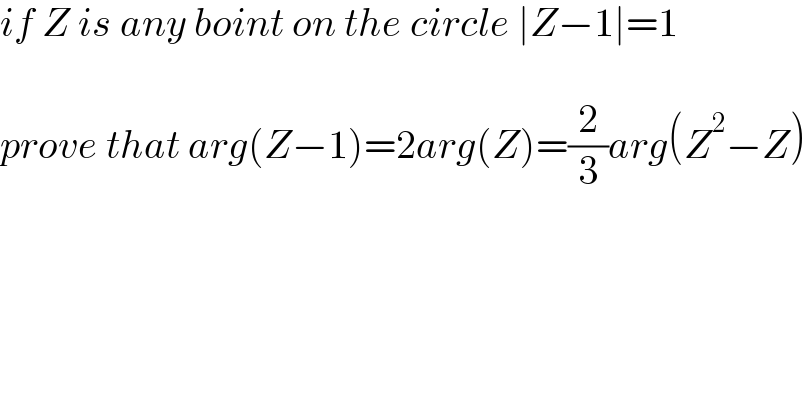
$${if}\:{Z}\:{is}\:{any}\:{boint}\:{on}\:{the}\:{circle}\:\mid{Z}−\mathrm{1}\mid=\mathrm{1} \\ $$$$ \\ $$$${prove}\:{that}\:{arg}\left({Z}−\mathrm{1}\right)=\mathrm{2}{arg}\left({Z}\right)=\frac{\mathrm{2}}{\mathrm{3}}{arg}\left({Z}^{\mathrm{2}} −{Z}\right) \\ $$
Commented by mohammad17 last updated on 23/Jan/21

$$????? \\ $$
Answered by mathmax by abdo last updated on 26/Jan/21
$$\mathrm{this}\:\mathrm{exercise}\:\mathrm{is}\:\mathrm{solved} \\ $$
