
Question Number 130132 by bait last updated on 22/Jan/21

$${solve}\:\int\int_{{G}} \left(\mathrm{7}{x}−{y}\right){dxdy},\:{where}\:{G}\:{is}\:{given}\:{by}\:{y}=\mathrm{0} \\ $$$${x}+\mathrm{2}{y}=\mathrm{3},\:{x}={y}^{\mathrm{2}} \\ $$$$ \\ $$$${i}\:{want}\:{to}\:{know}\:{if}\:{the}\:{integral}\:{below}\:{is}\:{a}\:{correct} \\ $$$${representation}\:{of}\:{the}\:{integral}\:{above}. \\ $$$$\:\left(\underset{\mathrm{0}} {\overset{\frac{\mathrm{3}}{\mathrm{2}}} {\int}}\underset{\mathrm{0}} {\overset{\frac{\mathrm{9}}{\mathrm{4}}} {\int}}\left(\mathrm{7}{x}−{y}\right){dxdy}\right). \\ $$
Answered by Ar Brandon last updated on 22/Jan/21
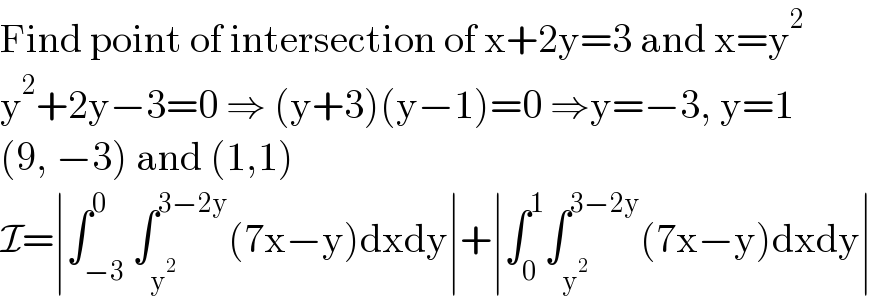
$$\mathrm{Find}\:\mathrm{point}\:\mathrm{of}\:\mathrm{intersection}\:\mathrm{of}\:\mathrm{x}+\mathrm{2y}=\mathrm{3}\:\mathrm{and}\:\mathrm{x}=\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{y}^{\mathrm{2}} +\mathrm{2y}−\mathrm{3}=\mathrm{0}\:\Rightarrow\:\left(\mathrm{y}+\mathrm{3}\right)\left(\mathrm{y}−\mathrm{1}\right)=\mathrm{0}\:\Rightarrow\mathrm{y}=−\mathrm{3},\:\mathrm{y}=\mathrm{1} \\ $$$$\left(\mathrm{9},\:−\mathrm{3}\right)\:\mathrm{and}\:\left(\mathrm{1},\mathrm{1}\right) \\ $$$$\mathcal{I}=\mid\int_{−\mathrm{3}} ^{\mathrm{0}} \int_{\mathrm{y}^{\mathrm{2}} } ^{\mathrm{3}−\mathrm{2y}} \left(\mathrm{7x}−\mathrm{y}\right)\mathrm{dxdy}\mid+\mid\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{y}^{\mathrm{2}} } ^{\mathrm{3}−\mathrm{2y}} \left(\mathrm{7x}−\mathrm{y}\right)\mathrm{dxdy}\mid \\ $$
Commented by bait last updated on 22/Jan/21
Thank you sir.
