
Question Number 130104 by mohammad17 last updated on 22/Jan/21
![find the key value [Arg(z)]for (2+i)^(1−i)](Q130104.png)
$${find}\:{the}\:{key}\:{value}\:\left[{Arg}\left({z}\right)\right]{for}\:\left(\mathrm{2}+{i}\right)^{\mathrm{1}−{i}} \\ $$
Answered by Olaf last updated on 22/Jan/21
![z = (2+i)^(1−i) Z = lnz = (1−i)ln(2+i) Z = (1−i)ln((√5)e^(iarctan(1/2)) ) Z = (1−i)[(1/2)ln5+iarctan(1/2)] Z = ((1/2)ln5+arctan(1/2))−i((1/2)ln5−arctan(1/2)) z = e^Z = (√5)e^(arctan(1/2)) e^(i(arctan(1/2)−(1/2)ln5)) Argz = arctan(1/2)−(1/2)ln5 (+2kπ) (or Argz = ((π−ln5)/2)−arctan2) (+2kπ)](Q130112.png)
$${z}\:=\:\left(\mathrm{2}+{i}\right)^{\mathrm{1}−{i}} \\ $$$$\mathrm{Z}\:=\:\mathrm{ln}{z}\:=\:\left(\mathrm{1}−{i}\right)\mathrm{ln}\left(\mathrm{2}+{i}\right) \\ $$$$\mathrm{Z}\:=\:\left(\mathrm{1}−{i}\right)\mathrm{ln}\left(\sqrt{\mathrm{5}}{e}^{{i}\mathrm{arctan}\frac{\mathrm{1}}{\mathrm{2}}} \right) \\ $$$$\mathrm{Z}\:=\:\left(\mathrm{1}−{i}\right)\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln5}+{i}\mathrm{arctan}\frac{\mathrm{1}}{\mathrm{2}}\right] \\ $$$$\mathrm{Z}\:=\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln5}+\mathrm{arctan}\frac{\mathrm{1}}{\mathrm{2}}\right)−{i}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln5}−\mathrm{arctan}\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${z}\:=\:{e}^{\mathrm{Z}} \:=\:\sqrt{\mathrm{5}}{e}^{\mathrm{arctan}\frac{\mathrm{1}}{\mathrm{2}}} {e}^{{i}\left(\mathrm{arctan}\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln5}\right)} \\ $$$$\mathrm{Ar}{gz}\:=\:\mathrm{arctan}\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln5}\:\left(+\mathrm{2}{k}\pi\right) \\ $$$$\left(\mathrm{or}\:\mathrm{Ar}{gz}\:=\:\frac{\pi−\mathrm{ln5}}{\mathrm{2}}−\mathrm{arctan2}\right)\:\left(+\mathrm{2}{k}\pi\right) \\ $$$$ \\ $$
Commented by mohammad17 last updated on 22/Jan/21
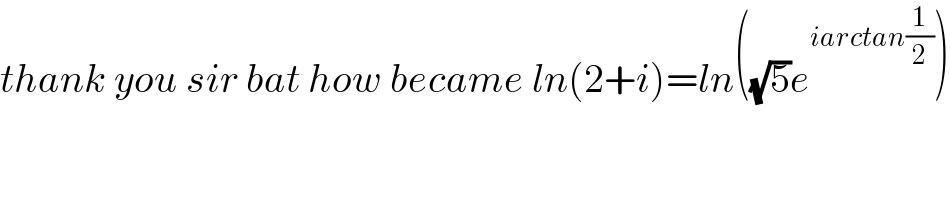
$${thank}\:{you}\:{sir}\:{bat}\:{how}\:{became}\:{ln}\left(\mathrm{2}+{i}\right)={ln}\left(\sqrt{\mathrm{5}}{e}^{{iarctan}\frac{\mathrm{1}}{\mathrm{2}}} \right) \\ $$
Commented by Olaf last updated on 22/Jan/21
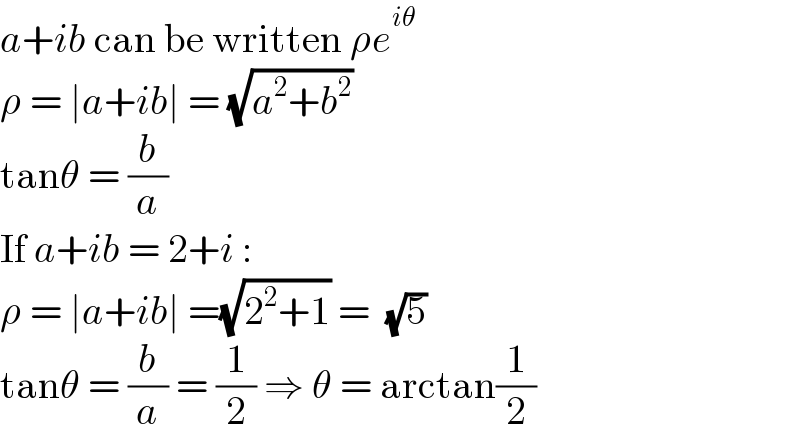
$${a}+{ib}\:\mathrm{can}\:\mathrm{be}\:\mathrm{written}\:\rho{e}^{{i}\theta} \\ $$$$\rho\:=\:\mid{a}+{ib}\mid\:=\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\theta\:=\:\frac{{b}}{{a}} \\ $$$$\mathrm{If}\:{a}+{ib}\:=\:\mathrm{2}+{i}\:: \\ $$$$\rho\:=\:\mid{a}+{ib}\mid\:=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}}\:=\:\:\sqrt{\mathrm{5}} \\ $$$$\mathrm{tan}\theta\:=\:\frac{{b}}{{a}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\theta\:=\:\mathrm{arctan}\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mohammad17 last updated on 22/Jan/21

$${thank}\:{you}\:{sir} \\ $$
