
Question Number 130087 by bobhans last updated on 22/Jan/21
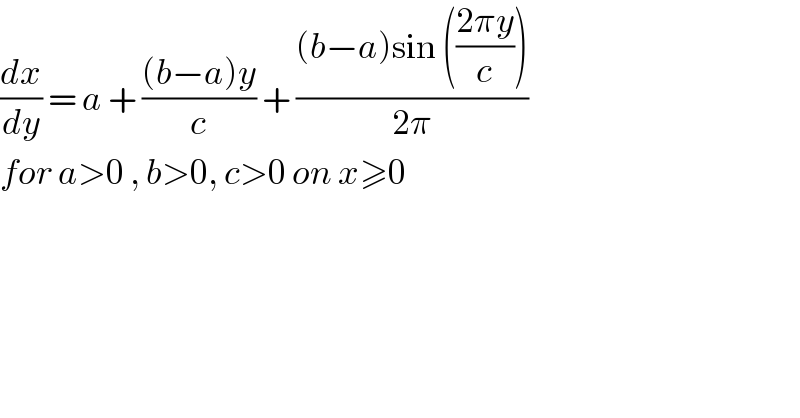
$$\frac{{dx}}{{dy}}\:=\:{a}\:+\:\frac{\left({b}−{a}\right){y}}{{c}}\:+\:\frac{\left({b}−{a}\right)\mathrm{sin}\:\left(\frac{\mathrm{2}\pi{y}}{{c}}\right)}{\mathrm{2}\pi} \\ $$ $${for}\:{a}>\mathrm{0}\:,\:{b}>\mathrm{0},\:{c}>\mathrm{0}\:{on}\:{x}\geqslant\mathrm{0}\: \\ $$
Answered by benjo_mathlover last updated on 22/Jan/21
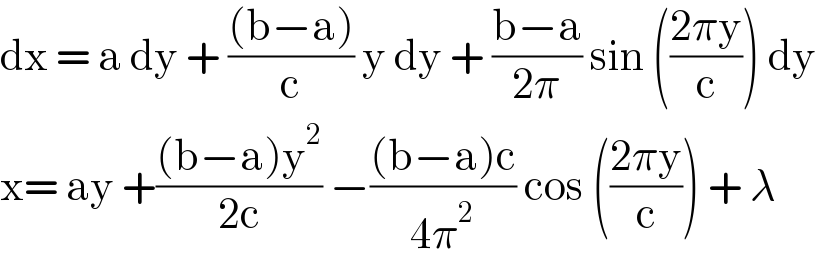
$$\mathrm{dx}\:=\:\mathrm{a}\:\mathrm{dy}\:+\:\frac{\left(\mathrm{b}−\mathrm{a}\right)}{\mathrm{c}}\:\mathrm{y}\:\mathrm{dy}\:+\:\frac{\mathrm{b}−\mathrm{a}}{\mathrm{2}\pi}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\pi\mathrm{y}}{\mathrm{c}}\right)\:\mathrm{dy} \\ $$ $$\mathrm{x}=\:\mathrm{ay}\:+\frac{\left(\mathrm{b}−\mathrm{a}\right)\mathrm{y}^{\mathrm{2}} }{\mathrm{2c}}\:−\frac{\left(\mathrm{b}−\mathrm{a}\right)\mathrm{c}}{\mathrm{4}\pi^{\mathrm{2}} }\:\mathrm{cos}\:\left(\frac{\mathrm{2}\pi\mathrm{y}}{\mathrm{c}}\right)\:+\:\lambda\: \\ $$
