
Question Number 13005 by 1630321995 last updated on 10/May/17

$${using}\:{De}\:{Moivre}\:{theorem}\:{solve}\:{the}\:{equation}\:\left({x}+\mathrm{1}\right)^{\mathrm{5}} +\left({x}−\mathrm{1}\right)^{\mathrm{5}} =\mathrm{0} \\ $$
Answered by mrW1 last updated on 10/May/17
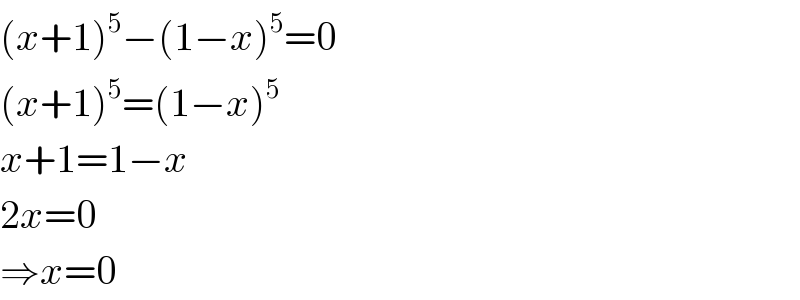
$$\left({x}+\mathrm{1}\right)^{\mathrm{5}} −\left(\mathrm{1}−{x}\right)^{\mathrm{5}} =\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{5}} =\left(\mathrm{1}−{x}\right)^{\mathrm{5}} \\ $$$${x}+\mathrm{1}=\mathrm{1}−{x} \\ $$$$\mathrm{2}{x}=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{0} \\ $$
