
Question Number 130036 by liberty last updated on 22/Jan/21
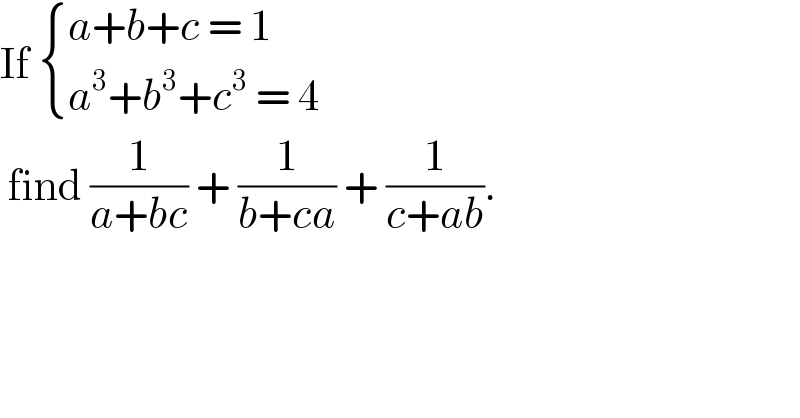
$$\mathrm{If}\:\begin{cases}{{a}+{b}+{c}\:=\:\mathrm{1}}\\{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \:=\:\mathrm{4}}\end{cases} \\ $$$$\:\mathrm{find}\:\frac{\mathrm{1}}{{a}+{bc}}\:+\:\frac{\mathrm{1}}{{b}+{ca}}\:+\:\frac{\mathrm{1}}{{c}+{ab}}. \\ $$
Answered by mnjuly1970 last updated on 22/Jan/21

$${solution}:\:\left\{_{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{4}} ^{{a}+{b}+{c}=\mathrm{1}} \right. \\ $$$$\:{K}=\frac{\mathrm{1}}{{a}+{bc}}+\frac{\mathrm{1}}{{b}+{ac}}\:+\frac{\mathrm{1}}{{c}+{ab}}=? \\ $$$${a}+{b}+{c}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\left({c}−\mathrm{1}\right)^{\mathrm{3}} =\mathrm{3}{ab}\left({c}−\mathrm{1}\right)\:\:\left({euler}\:\:{identity}\right) \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{c}^{\mathrm{2}} +\mathrm{3}{c}−\mathrm{1}=\mathrm{3}{abc}−\mathrm{3}{ab} \\ $$$$\mathrm{1}−{c}^{\mathrm{2}} +{c}={ab}\left({c}−\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\left({cyclic}\right) \\ $$$$\mathrm{1}=\left({c}−\mathrm{1}\right)\left({c}+{ab}\right)....\left(\mathrm{1}\right) \\ $$$$\therefore\:\mathrm{1}=\left({a}−\mathrm{1}\right)\left({a}+{bc}\right)....\left(\mathrm{2}\right) \\ $$$$\:\:\mathrm{1}=\left({b}−\mathrm{1}\right)\left({b}+{ac}\right)...\left(\mathrm{3}\right) \\ $$$$\:\therefore\:{K}=\frac{\mathrm{1}}{{a}+{bc}}+\frac{\mathrm{1}}{{b}+{ca}}\:+\frac{\mathrm{1}}{{c}+{ab}} \\ $$$$\:\:\:\:\:{K}\overset{\:\left(\mathrm{1}\right),\left(\mathrm{2}\right),\left(\mathrm{3}\right)} {=}{a}−\mathrm{1}+{b}−\mathrm{1}+{c}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{K}={a}+{b}+{c}−\mathrm{3}=\mathrm{1}−\mathrm{3}=−\mathrm{2}\:\:\checkmark \\ $$
Answered by EDWIN88 last updated on 22/Jan/21
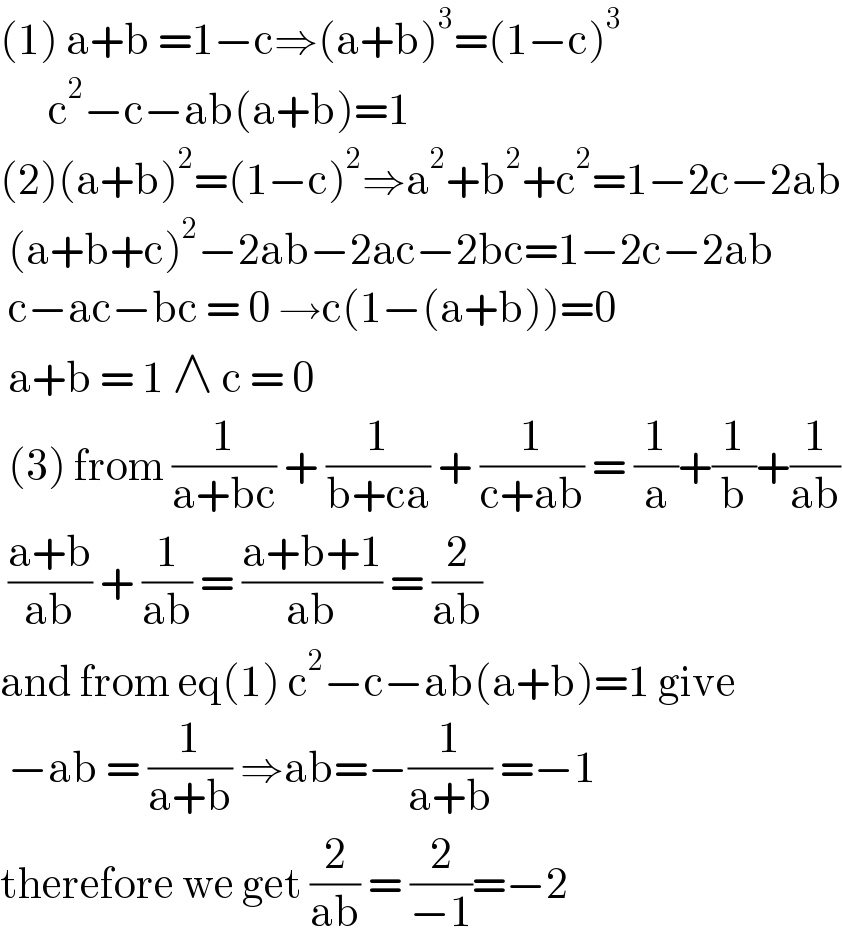
$$\left(\mathrm{1}\right)\:\mathrm{a}+\mathrm{b}\:=\mathrm{1}−\mathrm{c}\Rightarrow\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{3}} =\left(\mathrm{1}−\mathrm{c}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\mathrm{c}^{\mathrm{2}} −\mathrm{c}−\mathrm{ab}\left(\mathrm{a}+\mathrm{b}\right)=\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{c}\right)^{\mathrm{2}} \Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{1}−\mathrm{2c}−\mathrm{2ab} \\ $$$$\:\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)^{\mathrm{2}} −\mathrm{2ab}−\mathrm{2ac}−\mathrm{2bc}=\mathrm{1}−\mathrm{2c}−\mathrm{2ab} \\ $$$$\:\mathrm{c}−\mathrm{ac}−\mathrm{bc}\:=\:\mathrm{0}\:\rightarrow\mathrm{c}\left(\mathrm{1}−\left(\mathrm{a}+\mathrm{b}\right)\right)=\mathrm{0} \\ $$$$\:\mathrm{a}+\mathrm{b}\:=\:\mathrm{1}\:\wedge\:\mathrm{c}\:=\:\mathrm{0} \\ $$$$\:\left(\mathrm{3}\right)\:\mathrm{from}\:\frac{\mathrm{1}}{\mathrm{a}+\mathrm{bc}}\:+\:\frac{\mathrm{1}}{\mathrm{b}+\mathrm{ca}}\:+\:\frac{\mathrm{1}}{\mathrm{c}+\mathrm{ab}}\:=\:\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{b}}+\frac{\mathrm{1}}{\mathrm{ab}} \\ $$$$\:\frac{\mathrm{a}+\mathrm{b}}{\mathrm{ab}}\:+\:\frac{\mathrm{1}}{\mathrm{ab}}\:=\:\frac{\mathrm{a}+\mathrm{b}+\mathrm{1}}{\mathrm{ab}}\:=\:\frac{\mathrm{2}}{\mathrm{ab}} \\ $$$$\mathrm{and}\:\mathrm{from}\:\mathrm{eq}\left(\mathrm{1}\right)\:\mathrm{c}^{\mathrm{2}} −\mathrm{c}−\mathrm{ab}\left(\mathrm{a}+\mathrm{b}\right)=\mathrm{1}\:\mathrm{give} \\ $$$$\:−\mathrm{ab}\:=\:\frac{\mathrm{1}}{\mathrm{a}+\mathrm{b}}\:\Rightarrow\mathrm{ab}=−\frac{\mathrm{1}}{\mathrm{a}+\mathrm{b}}\:=−\mathrm{1} \\ $$$$\mathrm{therefore}\:\mathrm{we}\:\mathrm{get}\:\frac{\mathrm{2}}{\mathrm{ab}}\:=\:\frac{\mathrm{2}}{−\mathrm{1}}=−\mathrm{2} \\ $$
