
Question Number 130011 by mnjuly1970 last updated on 21/Jan/21
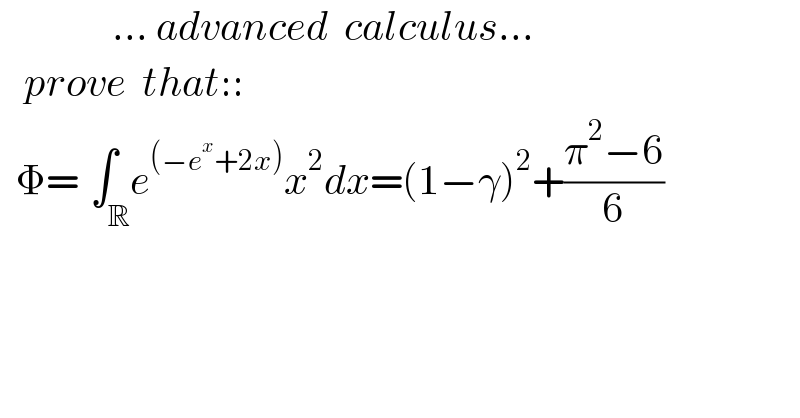
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\:{advanced}\:\:{calculus}... \\ $$$$\:\:\:{prove}\:\:{that}:: \\ $$$$\:\:\Phi=\underset{\:\:\:\:\:\mathbb{R}} {\int}{e}^{\left(−{e}^{{x}} +\mathrm{2}{x}\right)} {x}^{\mathrm{2}} {dx}=\left(\mathrm{1}−\gamma\right)^{\mathrm{2}} +\frac{\pi^{\mathrm{2}} −\mathrm{6}}{\mathrm{6}} \\ $$$$ \\ $$
Answered by mindispower last updated on 21/Jan/21

$${not}\:{integrabl}\:{over}\:\mathbb{R} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 21/Jan/21
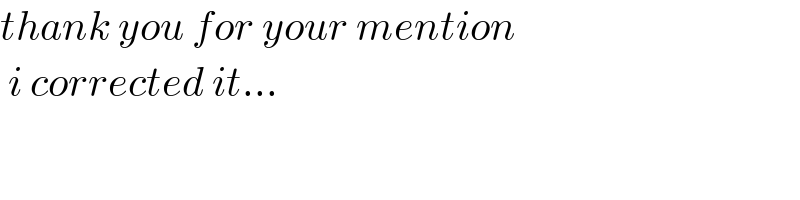
$${thank}\:{you}\:{for}\:{your}\:{mention} \\ $$$$\:{i}\:{corrected}\:{it}... \\ $$
Answered by mindispower last updated on 22/Jan/21
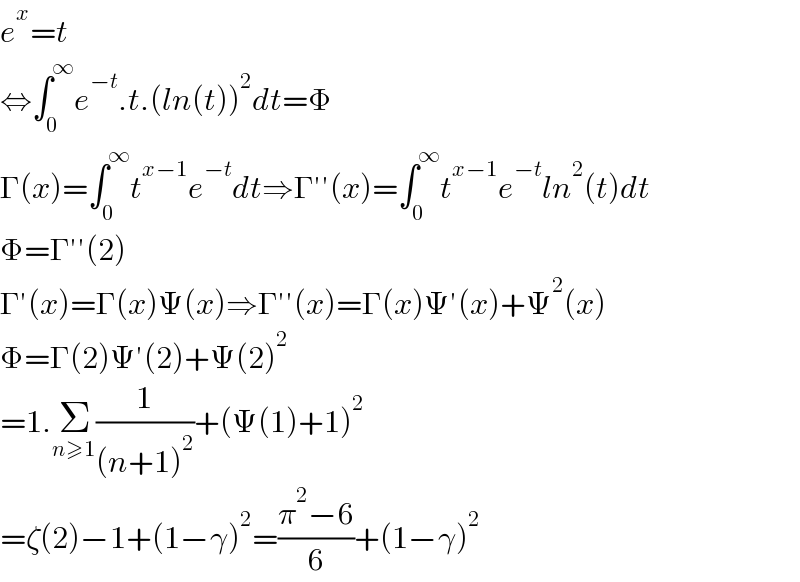
$${e}^{{x}} ={t} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} .{t}.\left({ln}\left({t}\right)\right)^{\mathrm{2}} {dt}=\Phi \\ $$$$\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt}\Rightarrow\Gamma''\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {ln}^{\mathrm{2}} \left({t}\right){dt} \\ $$$$\Phi=\Gamma''\left(\mathrm{2}\right) \\ $$$$\Gamma'\left({x}\right)=\Gamma\left({x}\right)\Psi\left({x}\right)\Rightarrow\Gamma''\left({x}\right)=\Gamma\left({x}\right)\Psi'\left({x}\right)+\Psi^{\mathrm{2}} \left({x}\right) \\ $$$$\Phi=\Gamma\left(\mathrm{2}\right)\Psi'\left(\mathrm{2}\right)+\Psi\left(\mathrm{2}\right)^{\mathrm{2}} \\ $$$$=\mathrm{1}.\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }+\left(\Psi\left(\mathrm{1}\right)+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\zeta\left(\mathrm{2}\right)−\mathrm{1}+\left(\mathrm{1}−\gamma\right)^{\mathrm{2}} =\frac{\pi^{\mathrm{2}} −\mathrm{6}}{\mathrm{6}}+\left(\mathrm{1}−\gamma\right)^{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 22/Jan/21
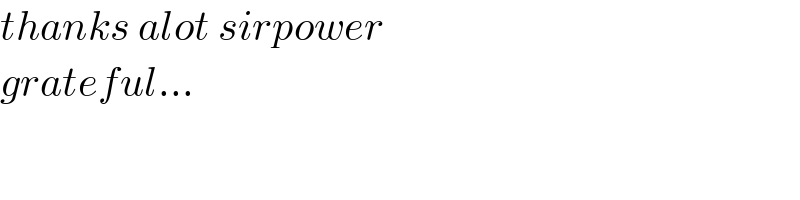
$${thanks}\:{alot}\:{sirpower}\: \\ $$$${grateful}... \\ $$
Commented by mindispower last updated on 23/Jan/21

$${pleasur}\:{sir} \\ $$
