
Question Number 129979 by liberty last updated on 21/Jan/21
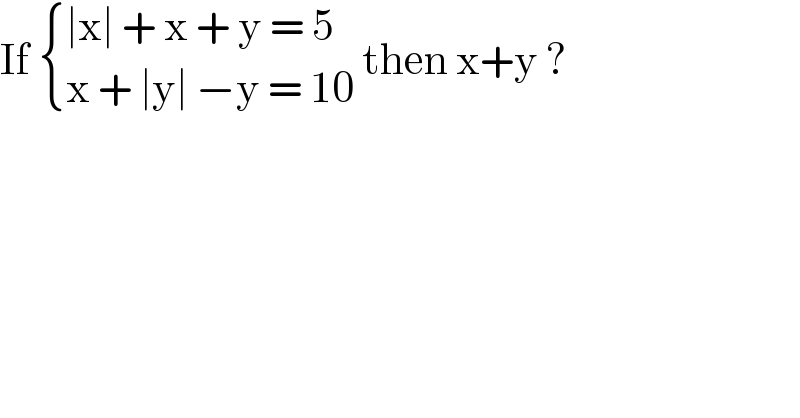
$$\mathrm{If}\:\begin{cases}{\mid\mathrm{x}\mid\:+\:\mathrm{x}\:+\:\mathrm{y}\:=\:\mathrm{5}}\\{\mathrm{x}\:+\:\mid\mathrm{y}\mid\:−\mathrm{y}\:=\:\mathrm{10}}\end{cases}\:\mathrm{then}\:\mathrm{x}+\mathrm{y}\:? \\ $$
Answered by MJS_new last updated on 21/Jan/21
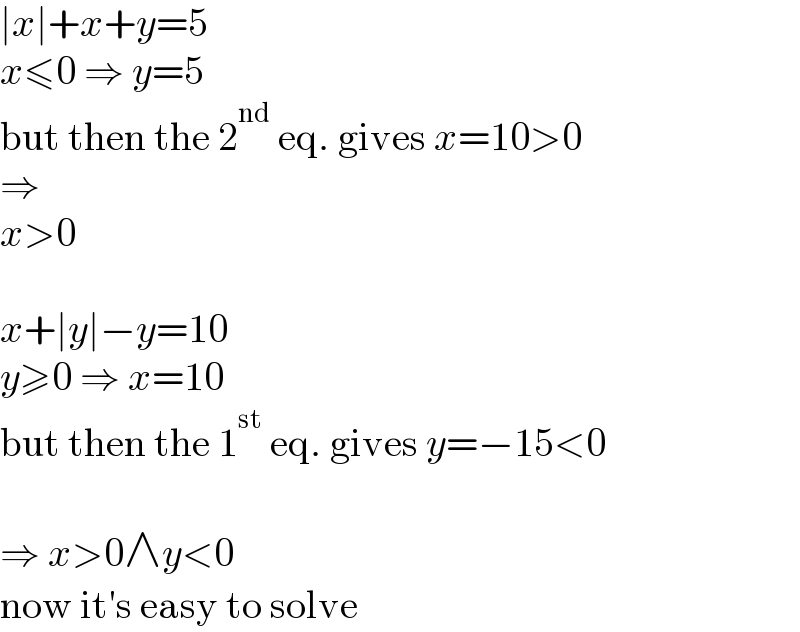
$$\mid{x}\mid+{x}+{y}=\mathrm{5} \\ $$$${x}\leqslant\mathrm{0}\:\Rightarrow\:{y}=\mathrm{5} \\ $$$$\mathrm{but}\:\mathrm{then}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{eq}.\:\mathrm{gives}\:{x}=\mathrm{10}>\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}>\mathrm{0} \\ $$$$ \\ $$$${x}+\mid{y}\mid−{y}=\mathrm{10} \\ $$$${y}\geqslant\mathrm{0}\:\Rightarrow\:{x}=\mathrm{10} \\ $$$$\mathrm{but}\:\mathrm{then}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{eq}.\:\mathrm{gives}\:{y}=−\mathrm{15}<\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow\:{x}>\mathrm{0}\wedge{y}<\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
Answered by EDWIN88 last updated on 21/Jan/21
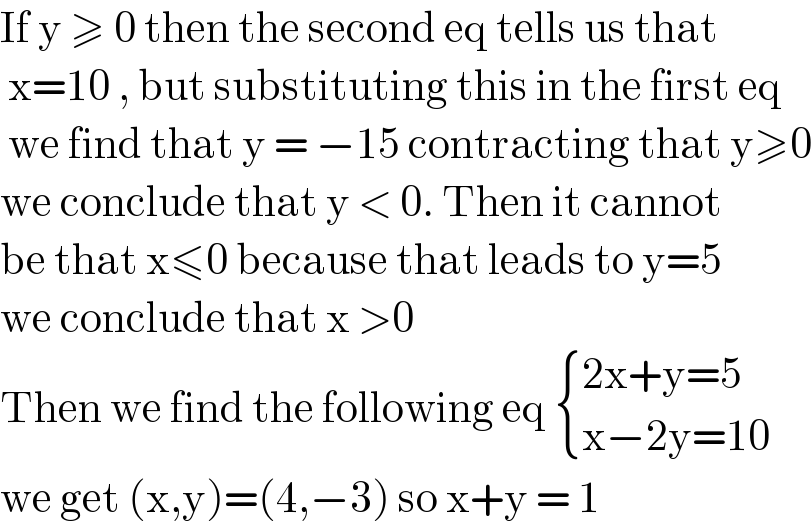
$$\mathrm{If}\:\mathrm{y}\:\geqslant\:\mathrm{0}\:\mathrm{then}\:\mathrm{the}\:\mathrm{second}\:\mathrm{eq}\:\mathrm{tells}\:\mathrm{us}\:\mathrm{that} \\ $$$$\:\mathrm{x}=\mathrm{10}\:,\:\mathrm{but}\:\mathrm{substituting}\:\mathrm{this}\:\mathrm{in}\:\mathrm{the}\:\mathrm{first}\:\mathrm{eq} \\ $$$$\:\mathrm{we}\:\mathrm{find}\:\mathrm{that}\:\mathrm{y}\:=\:−\mathrm{15}\:\mathrm{contracting}\:\mathrm{that}\:\mathrm{y}\geqslant\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{conclude}\:\mathrm{that}\:\mathrm{y}\:<\:\mathrm{0}.\:\mathrm{Then}\:\mathrm{it}\:\mathrm{cannot}\: \\ $$$$\mathrm{be}\:\mathrm{that}\:\mathrm{x}\leqslant\mathrm{0}\:\mathrm{because}\:\mathrm{that}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{y}=\mathrm{5} \\ $$$$\mathrm{we}\:\mathrm{conclude}\:\mathrm{that}\:\mathrm{x}\:>\mathrm{0}\: \\ $$$$\mathrm{Then}\:\mathrm{we}\:\mathrm{find}\:\mathrm{the}\:\mathrm{following}\:\mathrm{eq}\:\begin{cases}{\mathrm{2x}+\mathrm{y}=\mathrm{5}}\\{\mathrm{x}−\mathrm{2y}=\mathrm{10}}\end{cases} \\ $$$$\mathrm{we}\:\mathrm{get}\:\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{4},−\mathrm{3}\right)\:\mathrm{so}\:\mathrm{x}+\mathrm{y}\:=\:\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 21/Jan/21
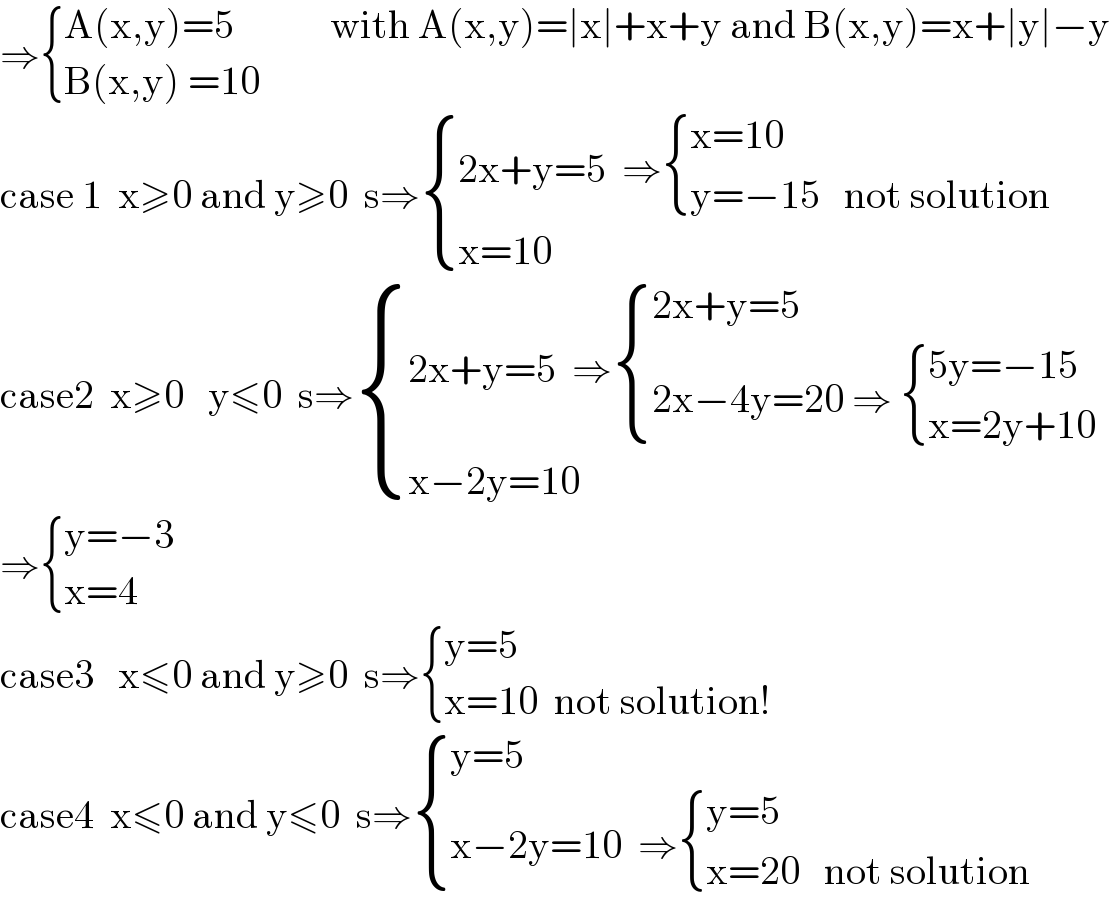
$$\Rightarrow\begin{cases}{\mathrm{A}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{with}\:\mathrm{A}\left(\mathrm{x},\mathrm{y}\right)=\mid\mathrm{x}\mid+\mathrm{x}+\mathrm{y}\:\mathrm{and}\:\mathrm{B}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}+\mid\mathrm{y}\mid−\mathrm{y}}\\{\mathrm{B}\left(\mathrm{x},\mathrm{y}\right)\:=\mathrm{10}}\end{cases} \\ $$$$\mathrm{case}\:\mathrm{1}\:\:\mathrm{x}\geqslant\mathrm{0}\:\mathrm{and}\:\mathrm{y}\geqslant\mathrm{0}\:\:\mathrm{s}\Rightarrow\begin{cases}{\mathrm{2x}+\mathrm{y}=\mathrm{5}\:\:\Rightarrow\begin{cases}{\mathrm{x}=\mathrm{10}\:\:\:}\\{\mathrm{y}=−\mathrm{15}\:\:\:\mathrm{not}\:\mathrm{solution}}\end{cases}}\\{\mathrm{x}=\mathrm{10}}\end{cases} \\ $$$$\mathrm{case2}\:\:\mathrm{x}\geqslant\mathrm{0}\:\:\:\mathrm{y}\leqslant\mathrm{0}\:\:\mathrm{s}\Rightarrow\begin{cases}{\mathrm{2x}+\mathrm{y}=\mathrm{5}\:\:\Rightarrow\begin{cases}{\mathrm{2x}+\mathrm{y}=\mathrm{5}}\\{\mathrm{2x}−\mathrm{4y}=\mathrm{20}\:\Rightarrow\:\begin{cases}{\mathrm{5y}=−\mathrm{15}}\\{\mathrm{x}=\mathrm{2y}+\mathrm{10}}\end{cases}}\end{cases}}\\{\mathrm{x}−\mathrm{2y}=\mathrm{10}\:}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{y}=−\mathrm{3}\:\:\:\:\:}\\{\mathrm{x}=\mathrm{4}}\end{cases} \\ $$$$\mathrm{case3}\:\:\:\mathrm{x}\leqslant\mathrm{0}\:\mathrm{and}\:\mathrm{y}\geqslant\mathrm{0}\:\:\mathrm{s}\Rightarrow\begin{cases}{\mathrm{y}=\mathrm{5}\:\:\:\:}\\{\mathrm{x}=\mathrm{10}\:\:\mathrm{not}\:\mathrm{solution}!}\end{cases} \\ $$$$\mathrm{case4}\:\:\mathrm{x}\leqslant\mathrm{0}\:\mathrm{and}\:\mathrm{y}\leqslant\mathrm{0}\:\:\mathrm{s}\Rightarrow\begin{cases}{\mathrm{y}=\mathrm{5}}\\{\mathrm{x}−\mathrm{2y}=\mathrm{10}\:\:\Rightarrow\begin{cases}{\mathrm{y}=\mathrm{5}}\\{\mathrm{x}=\mathrm{20}\:\:\:\mathrm{not}\:\mathrm{solution}}\end{cases}}\end{cases} \\ $$
