
Question Number 129978 by MJS_new last updated on 21/Jan/21
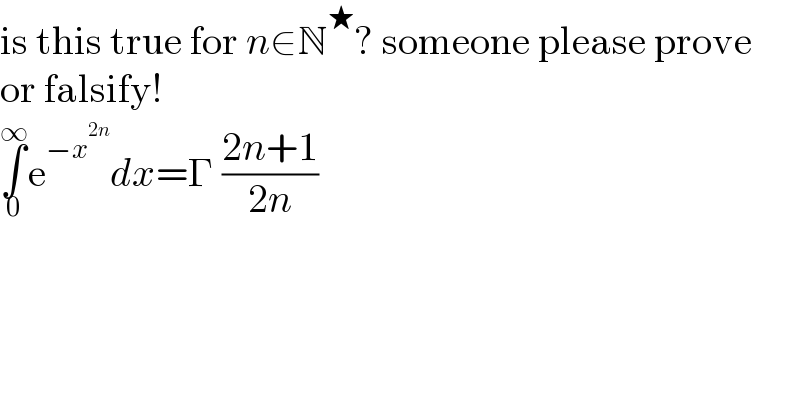
$$\mathrm{is}\:\mathrm{this}\:\mathrm{true}\:\mathrm{for}\:{n}\in\mathbb{N}^{\bigstar} ?\:\mathrm{someone}\:\mathrm{please}\:\mathrm{prove} \\ $$$$\mathrm{or}\:\mathrm{falsify}! \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−{x}^{\mathrm{2}{n}} } {dx}=\Gamma\:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}} \\ $$
Answered by Dwaipayan Shikari last updated on 21/Jan/21
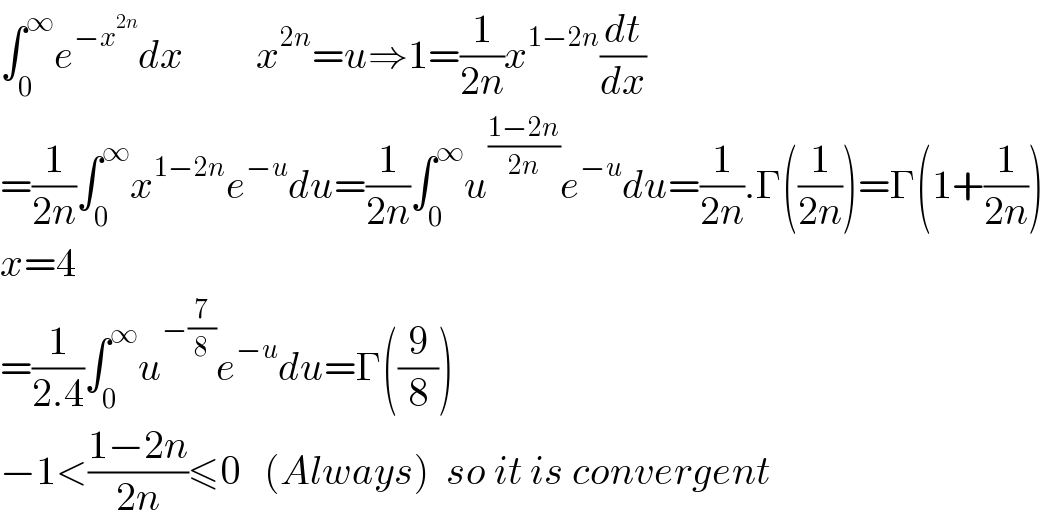
$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}{n}} } {dx}\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}{n}} ={u}\Rightarrow\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}{n}}{x}^{\mathrm{1}−\mathrm{2}{n}} \frac{{dt}}{{dx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{n}}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{1}−\mathrm{2}{n}} {e}^{−{u}} {du}=\frac{\mathrm{1}}{\mathrm{2}{n}}\int_{\mathrm{0}} ^{\infty} {u}^{\frac{\mathrm{1}−\mathrm{2}{n}}{\mathrm{2}{n}}} {e}^{−{u}} {du}=\frac{\mathrm{1}}{\mathrm{2}{n}}.\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}{n}}\right)=\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$${x}=\mathrm{4} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}}\int_{\mathrm{0}} ^{\infty} {u}^{−\frac{\mathrm{7}}{\mathrm{8}}} {e}^{−{u}} {du}=\Gamma\left(\frac{\mathrm{9}}{\mathrm{8}}\right) \\ $$$$−\mathrm{1}<\frac{\mathrm{1}−\mathrm{2}{n}}{\mathrm{2}{n}}\leqslant\mathrm{0}\:\:\:\left({Always}\right)\:\:{so}\:{it}\:{is}\:{convergent} \\ $$
Commented by MJS_new last updated on 21/Jan/21
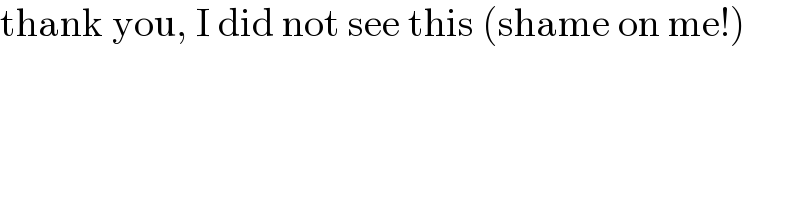
$$\mathrm{thank}\:\mathrm{you},\:\mathrm{I}\:\mathrm{did}\:\mathrm{not}\:\mathrm{see}\:\mathrm{this}\:\left(\mathrm{shame}\:\mathrm{on}\:\mathrm{me}!\right) \\ $$
Commented by Dwaipayan Shikari last updated on 21/Jan/21
�� sir MJS
