
Question Number 129938 by stelor last updated on 21/Jan/21
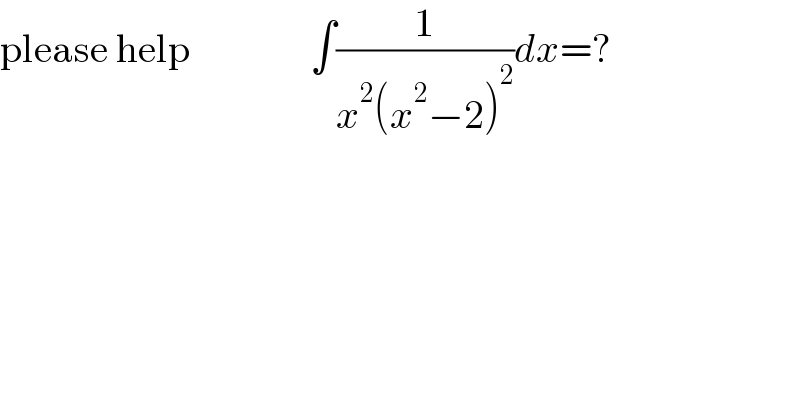
$$\mathrm{please}\:\mathrm{help}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }{dx}=? \\ $$$$ \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 21/Jan/21
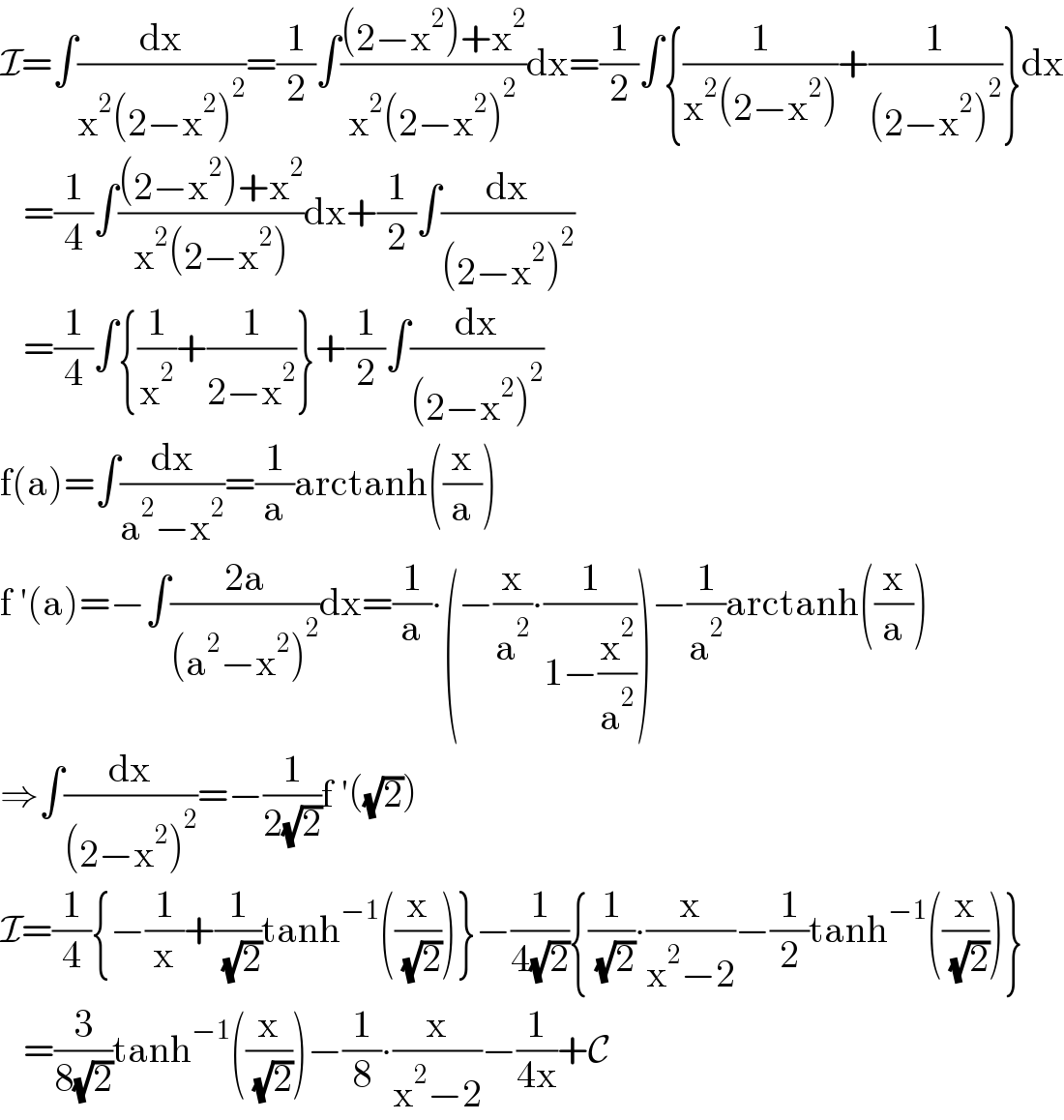
$$\mathcal{I}=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)+\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right\}\mathrm{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)+\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int\left\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }\right\}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int\frac{\mathrm{dx}}{\mathrm{a}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{arctanh}\left(\frac{\mathrm{x}}{\mathrm{a}}\right) \\ $$$$\mathrm{f}\:'\left(\mathrm{a}\right)=−\int\frac{\mathrm{2a}}{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{a}}\centerdot\left(−\frac{\mathrm{x}}{\mathrm{a}^{\mathrm{2}} }\centerdot\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right)−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\mathrm{arctanh}\left(\frac{\mathrm{x}}{\mathrm{a}}\right) \\ $$$$\Rightarrow\int\frac{\mathrm{dx}}{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{f}\:'\left(\sqrt{\mathrm{2}}\right) \\ $$$$\mathcal{I}=\frac{\mathrm{1}}{\mathrm{4}}\left\{−\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)\right\}−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\centerdot\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)\right\} \\ $$$$\:\:\:=\frac{\mathrm{3}}{\mathrm{8}\sqrt{\mathrm{2}}}\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{8}}\centerdot\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4x}}+\mathcal{C} \\ $$
Commented by stelor last updated on 21/Jan/21

$$\mathrm{merci}−− \\ $$
Answered by Ar Brandon last updated on 21/Jan/21

$$\mathcal{I}=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }\:,\:\mathrm{x}=\sqrt{\mathrm{2}}\mathrm{sin}\theta \\ $$$$\:\:\:=\int\frac{\sqrt{\mathrm{2}}\mathrm{cos}\theta\mathrm{d}\theta}{\mathrm{2sin}^{\mathrm{2}} \theta\centerdot\mathrm{4}\left(\mathrm{sin}^{\mathrm{2}} \theta−\mathrm{1}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\int\frac{\mathrm{d}\theta}{\mathrm{sin}^{\mathrm{2}} \theta\mathrm{cos}^{\mathrm{3}} \theta} \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}}{\:\mathrm{8}}\int\left\{\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \theta\mathrm{cos}\theta}+\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{3}} \theta}\right\}\mathrm{d}\theta=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\int\left\{\frac{\mathrm{cos}\theta}{\mathrm{sin}^{\mathrm{2}} \theta}+\frac{\mathrm{1}}{\mathrm{cos}\theta}+\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{3}} \theta}\right\}\mathrm{d}\theta \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\left\{−\frac{\mathrm{1}}{\mathrm{sin}\theta}+\mathrm{ln}\mid\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\mid\right\}+\frac{\sqrt{\mathrm{2}}}{\:\mathrm{8}}\int\frac{\mathrm{d}\theta}{\mathrm{cos}^{\mathrm{3}} \theta} \\ $$$$\int\frac{\mathrm{d}\theta}{\mathrm{cos}^{\mathrm{3}} \theta}=\int\frac{\mathrm{cos}\theta}{\mathrm{cos}^{\mathrm{4}} \theta}\mathrm{d}\theta=\int\frac{\mathrm{cos}\theta}{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\mathrm{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int\frac{\mathrm{du}}{\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{2}} }=\int\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{4}} −\mathrm{2u}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\frac{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)−\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{u}^{\mathrm{4}} −\mathrm{2u}^{\mathrm{2}} +\mathrm{1}}\right\}\mathrm{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}{\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} }−\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} −\mathrm{4}}\right\}\mathrm{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\int\frac{\mathrm{dp}}{\mathrm{p}^{\mathrm{2}} }−\int\frac{\mathrm{dq}}{\mathrm{q}^{\mathrm{2}} −\mathrm{4}}\right\}=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\frac{\mathrm{1}}{\mathrm{p}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\frac{\mathrm{q}+\mathrm{2}}{\mathrm{q}−\mathrm{2}}\mid\right\}+\mathrm{C} \\ $$
Commented by liberty last updated on 21/Jan/21
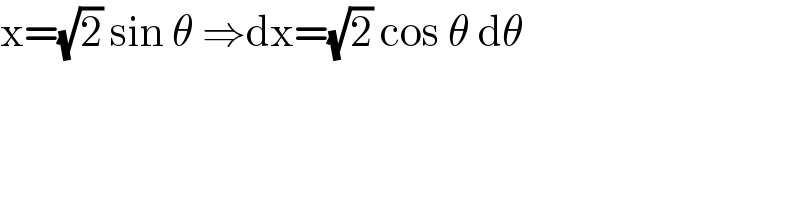
$$\mathrm{x}=\sqrt{\mathrm{2}}\:\mathrm{sin}\:\theta\:\Rightarrow\mathrm{dx}=\sqrt{\mathrm{2}}\:\mathrm{cos}\:\theta\:\mathrm{d}\theta \\ $$
Commented by Ar Brandon last updated on 21/Jan/21
Yeah, you're right. Thanks for remark.
Answered by MJS_new last updated on 21/Jan/21
![∫(dx/(x^2 (x^2 −2)^2 ))= [Ostrogradski′s Method] =−((3x^2 −4)/(8x(x^2 −2)))−(3/8)∫(dx/(x^2 −2))= =−((3x^2 −4)/(8x(x^2 −2)))−((3(√2))/(32))∫(1/(x+(√2)))−(1/(x−(√2)))dx= =−((3x^2 −4)/(8x(x^2 −2)))−((3(√2))/(32))(ln ∣x+(√2)∣ −ln ∣x−(√2)∣)= =−((3x^2 −4)/(8x(x^2 −2)))−((3(√2))/(32))ln ∣((x+(√2))/(x−(√2)))∣ +C](Q129960.png)
$$\int\frac{{dx}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{8}{x}\left({x}^{\mathrm{2}} −\mathrm{2}\right)}−\frac{\mathrm{3}}{\mathrm{8}}\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}}= \\ $$$$=−\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{8}{x}\left({x}^{\mathrm{2}} −\mathrm{2}\right)}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\int\frac{\mathrm{1}}{{x}+\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{{x}−\sqrt{\mathrm{2}}}{dx}= \\ $$$$=−\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{8}{x}\left({x}^{\mathrm{2}} −\mathrm{2}\right)}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\left(\mathrm{ln}\:\mid{x}+\sqrt{\mathrm{2}}\mid\:−\mathrm{ln}\:\mid{x}−\sqrt{\mathrm{2}}\mid\right)= \\ $$$$=−\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{8}{x}\left({x}^{\mathrm{2}} −\mathrm{2}\right)}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\mathrm{ln}\:\mid\frac{{x}+\sqrt{\mathrm{2}}}{{x}−\sqrt{\mathrm{2}}}\mid\:+{C} \\ $$
Answered by mathmax by abdo last updated on 21/Jan/21
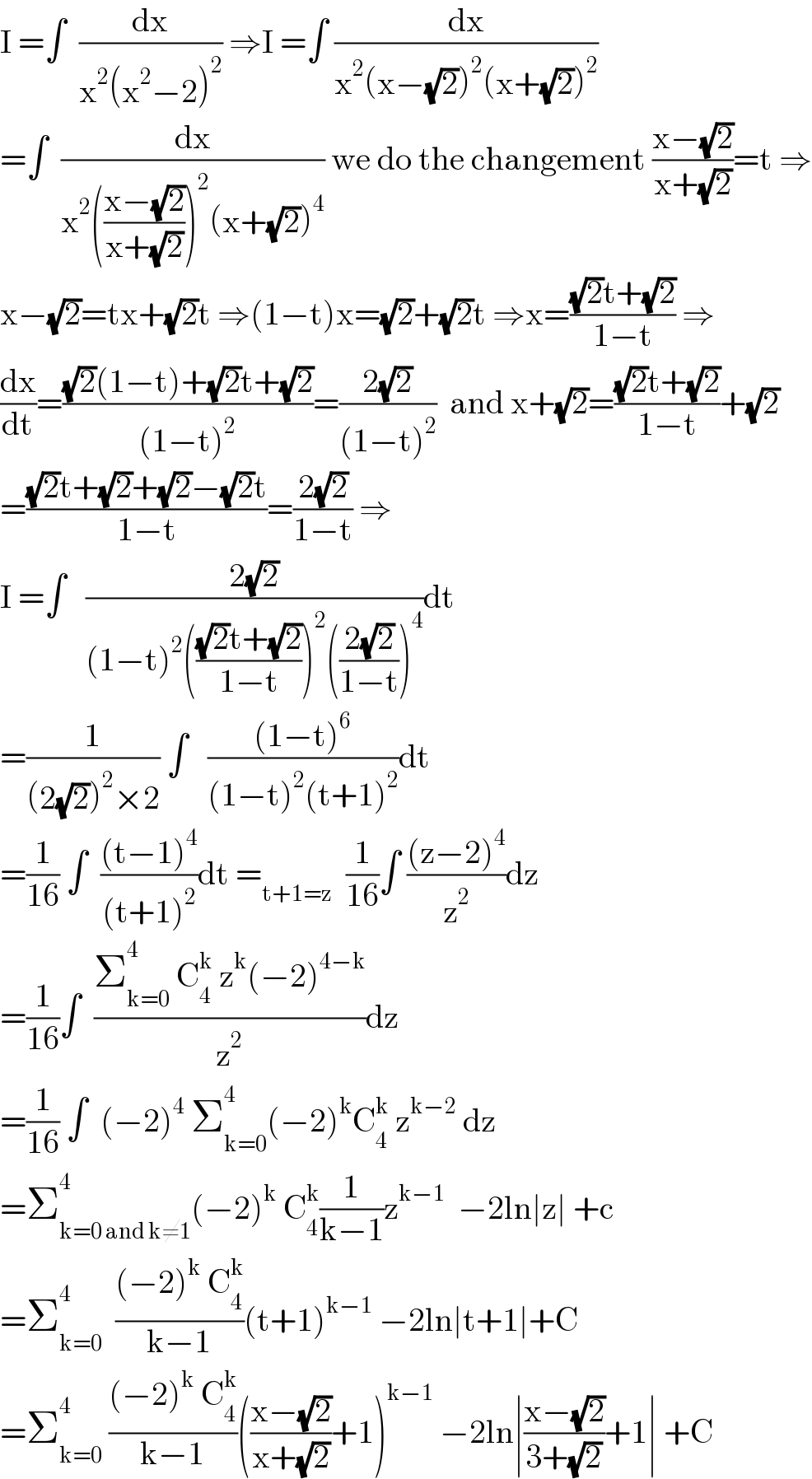
$$\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{I}\:=\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{x}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\frac{\mathrm{x}−\sqrt{\mathrm{2}}}{\mathrm{x}+\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \left(\mathrm{x}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} }\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{x}−\sqrt{\mathrm{2}}}{\mathrm{x}+\sqrt{\mathrm{2}}}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{x}−\sqrt{\mathrm{2}}=\mathrm{tx}+\sqrt{\mathrm{2}}\mathrm{t}\:\Rightarrow\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}=\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}\mathrm{t}\:\Rightarrow\mathrm{x}=\frac{\sqrt{\mathrm{2}}\mathrm{t}+\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow \\ $$$$\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\sqrt{\mathrm{2}}\left(\mathrm{1}−\mathrm{t}\right)+\sqrt{\mathrm{2}}\mathrm{t}+\sqrt{\mathrm{2}}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\:\:\mathrm{and}\:\mathrm{x}+\sqrt{\mathrm{2}}=\frac{\sqrt{\mathrm{2}}\mathrm{t}+\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{t}}+\sqrt{\mathrm{2}} \\ $$$$=\frac{\sqrt{\mathrm{2}}\mathrm{t}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}}\mathrm{t}}{\mathrm{1}−\mathrm{t}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} \left(\frac{\sqrt{\mathrm{2}}\mathrm{t}+\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{2}} \left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{4}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} ×\mathrm{2}}\:\int\:\:\:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{6}} }{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4}} }{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}\:=_{\mathrm{t}+\mathrm{1}=\mathrm{z}} \:\:\frac{\mathrm{1}}{\mathrm{16}}\int\:\frac{\left(\mathrm{z}−\mathrm{2}\right)^{\mathrm{4}} }{\mathrm{z}^{\mathrm{2}} }\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\int\:\:\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\mathrm{z}^{\mathrm{k}} \left(−\mathrm{2}\right)^{\mathrm{4}−\mathrm{k}} }{\mathrm{z}^{\mathrm{2}} }\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\:\left(−\mathrm{2}\right)^{\mathrm{4}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \left(−\mathrm{2}\right)^{\mathrm{k}} \mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\mathrm{z}^{\mathrm{k}−\mathrm{2}} \:\mathrm{dz} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{1}} ^{\mathrm{4}} \left(−\mathrm{2}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \frac{\mathrm{1}}{\mathrm{k}−\mathrm{1}}\mathrm{z}^{\mathrm{k}−\mathrm{1}} \:\:−\mathrm{2ln}\mid\mathrm{z}\mid\:+\mathrm{c}\:\:\:\: \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\:\frac{\left(−\mathrm{2}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{1}}\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \:−\mathrm{2ln}\mid\mathrm{t}+\mathrm{1}\mid+\mathrm{C} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\left(−\mathrm{2}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{1}}\left(\frac{\mathrm{x}−\sqrt{\mathrm{2}}}{\mathrm{x}+\sqrt{\mathrm{2}}}+\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \:−\mathrm{2ln}\mid\frac{\mathrm{x}−\sqrt{\mathrm{2}}}{\mathrm{3}+\sqrt{\mathrm{2}}}+\mathrm{1}\mid\:+\mathrm{C} \\ $$
Commented by mathmax by abdo last updated on 21/Jan/21

$$\mathrm{k}\neq\mathrm{1} \\ $$
