
Question Number 129874 by mohammad17 last updated on 20/Jan/21

Commented by mohammad17 last updated on 20/Jan/21

$${pleas}\:{sir}\:{help}\:{me} \\ $$
Answered by liberty last updated on 21/Jan/21
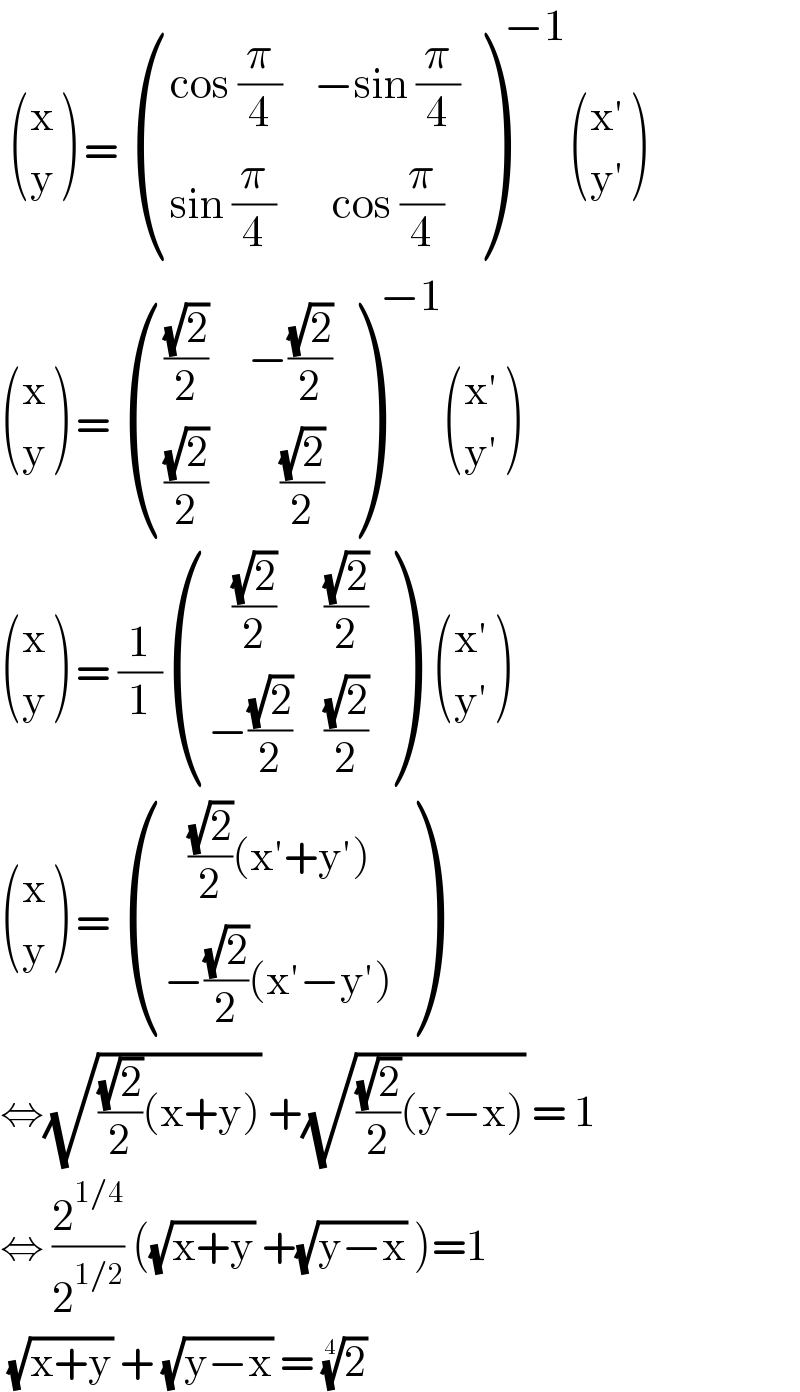
$$\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{cos}\:\frac{\pi}{\mathrm{4}}\:\:\:\:−\mathrm{sin}\:\frac{\pi}{\mathrm{4}}}\\{\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\:\:\:\:\:\:\:\mathrm{cos}\:\frac{\pi}{\mathrm{4}}}\end{pmatrix}^{−\mathrm{1}} \begin{pmatrix}{\mathrm{x}'}\\{\mathrm{y}'}\end{pmatrix} \\ $$$$\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}\:=\:\begin{pmatrix}{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\:\:\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\\{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\end{pmatrix}^{−\mathrm{1}} \begin{pmatrix}{\mathrm{x}'}\\{\mathrm{y}'}\end{pmatrix} \\ $$$$\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}\:=\:\frac{\mathrm{1}}{\mathrm{1}}\begin{pmatrix}{\:\:\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\:\:\:\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\\{−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\:\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\end{pmatrix}\:\:\begin{pmatrix}{\mathrm{x}'}\\{\mathrm{y}'}\end{pmatrix} \\ $$$$\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}\:=\:\begin{pmatrix}{\:\:\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{x}'+\mathrm{y}'\right)}\\{−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{x}'−\mathrm{y}'\right)}\end{pmatrix} \\ $$$$\Leftrightarrow\sqrt{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{x}+\mathrm{y}\right)}\:+\sqrt{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{y}−\mathrm{x}\right)}\:=\:\mathrm{1} \\ $$$$\Leftrightarrow\:\frac{\mathrm{2}^{\mathrm{1}/\mathrm{4}} }{\mathrm{2}^{\mathrm{1}/\mathrm{2}} }\:\left(\sqrt{\mathrm{x}+\mathrm{y}}\:+\sqrt{\mathrm{y}−\mathrm{x}}\:\right)=\mathrm{1} \\ $$$$\:\sqrt{\mathrm{x}+\mathrm{y}}\:+\:\sqrt{\mathrm{y}−\mathrm{x}}\:=\:\sqrt[{\mathrm{4}}]{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 20/Jan/21

$$\mathrm{error}:\:\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\sqrt{{x}+{y}}+\sqrt{{y}−{x}}=\sqrt[{\mathrm{4}}]{\mathrm{2}} \\ $$$$\sqrt{{x}}+\sqrt{{y}}=\mathrm{1}\:\Leftrightarrow\:{y}=\left(\mathrm{1}−\sqrt{{x}}\right)^{\mathrm{2}} =\mathrm{1}+{x}−\mathrm{2}\sqrt{{x}} \\ $$$$\:\:\:\:\:\mathrm{defined}\:\mathrm{for}\:{y}\geqslant\mathrm{0}\wedge{x}\geqslant\mathrm{0} \\ $$$$\sqrt{{x}+{y}}+\sqrt{{y}−{x}}=\sqrt[{\mathrm{4}}]{\mathrm{2}}\:\Leftrightarrow\:{y}=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:\:\:\:\:\mathrm{the}\:\mathrm{endpoint}\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{1}}\end{pmatrix}\:\mathrm{of}\:\mathrm{the}\:\mathrm{first}\:\mathrm{graph} \\ $$$$\:\:\:\:\:\mathrm{becomes}\:\begin{pmatrix}{−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\\{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\end{pmatrix}\:\:\Rightarrow\:\mathrm{defined}\:\mathrm{for}\:{x}\geqslant−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{part}\:\mathrm{of}\:\mathrm{a}\:\mathrm{parabola} \\ $$
Commented by bemath last updated on 21/Jan/21
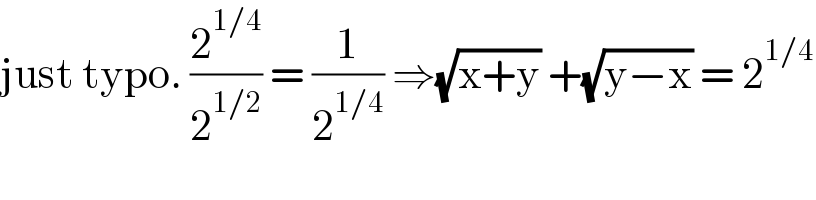
$$\mathrm{just}\:\mathrm{typo}.\:\frac{\mathrm{2}^{\mathrm{1}/\mathrm{4}} }{\mathrm{2}^{\mathrm{1}/\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}/\mathrm{4}} }\:\Rightarrow\sqrt{\mathrm{x}+\mathrm{y}}\:+\sqrt{\mathrm{y}−\mathrm{x}}\:=\:\mathrm{2}^{\mathrm{1}/\mathrm{4}} \\ $$
