
Question Number 129855 by liberty last updated on 20/Jan/21
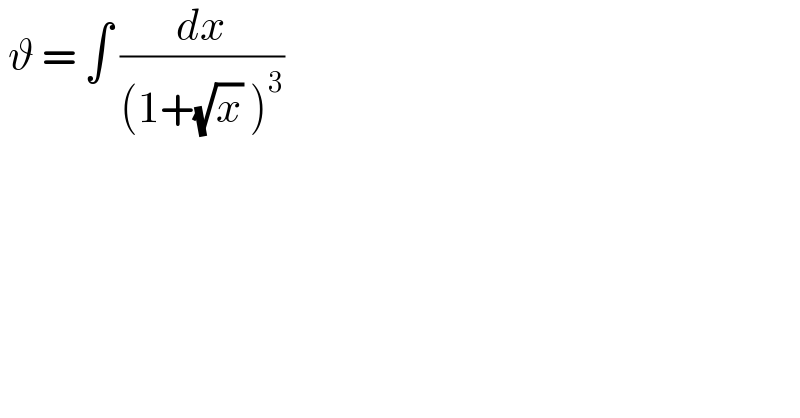
$$\:\vartheta\:=\:\int\:\frac{{dx}}{\left(\mathrm{1}+\sqrt{{x}}\:\right)^{\mathrm{3}} } \\ $$
Answered by EDWIN88 last updated on 20/Jan/21
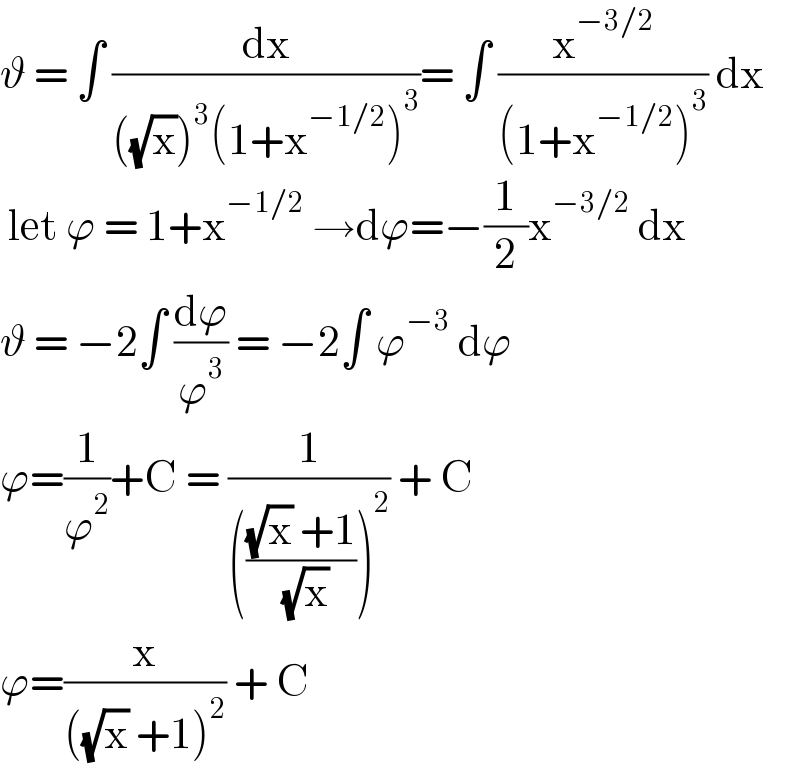
$$\vartheta\:=\:\int\:\frac{\mathrm{dx}}{\left(\sqrt{\mathrm{x}}\right)^{\mathrm{3}} \left(\mathrm{1}+\mathrm{x}^{−\mathrm{1}/\mathrm{2}} \right)^{\mathrm{3}} }=\:\int\:\frac{\mathrm{x}^{−\mathrm{3}/\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}^{−\mathrm{1}/\mathrm{2}} \right)^{\mathrm{3}} }\:\mathrm{dx} \\ $$$$\:\mathrm{let}\:\varphi\:=\:\mathrm{1}+\mathrm{x}^{−\mathrm{1}/\mathrm{2}} \:\rightarrow\mathrm{d}\varphi=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{−\mathrm{3}/\mathrm{2}} \:\mathrm{dx} \\ $$$$\vartheta\:=\:−\mathrm{2}\int\:\frac{\mathrm{d}\varphi}{\varphi^{\mathrm{3}} }\:=\:−\mathrm{2}\int\:\varphi^{−\mathrm{3}} \:\mathrm{d}\varphi \\ $$$$\varphi=\frac{\mathrm{1}}{\varphi^{\mathrm{2}} }+\mathrm{C}\:=\:\frac{\mathrm{1}}{\left(\frac{\sqrt{\mathrm{x}}\:+\mathrm{1}}{\:\sqrt{\mathrm{x}}}\right)^{\mathrm{2}} }\:+\:\mathrm{C} \\ $$$$\varphi=\frac{\mathrm{x}}{\left(\sqrt{\mathrm{x}}\:+\mathrm{1}\right)^{\mathrm{2}} }\:+\:\mathrm{C}\: \\ $$
Answered by stelor last updated on 20/Jan/21
![let u =(√x) so, du=(1/(2(√x)))dx = du = (1/(2u))dx v = ∫((2udu)/((1+u)^3 )) where u = (√x) let t = 1+u so, du=dt v =2∫(((t−1))/t^3 )dt where t = u−1= (√x)−1 v=2[∫((1/t^2 )−(1/t^3 ))dt] =2(−(1/t)+(1/(2t^2 )) + c ) v = 2(−(1/( (√x)−1))+(1/(2((√x)−1)^2 )) + c) v= ((3−2(√x))/(((√x)−1)^2 )) + c](Q129894.png)
$$\:\mathrm{let}\:{u}\:=\sqrt{{x}}\:\:\:\:\:{so},\:\:{du}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}{dx}\:=\:{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}{u}}{dx} \\ $$$${v}\:=\:\int\frac{\mathrm{2udu}}{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{3}} }\:\:{where}\:{u}\:=\:\sqrt{{x}} \\ $$$${let}\:{t}\:=\:\mathrm{1}+{u}\:\:{so},\:\mathrm{du}=\mathrm{dt} \\ $$$${v}\:=\mathrm{2}\int\frac{\left({t}−\mathrm{1}\right)}{{t}^{\mathrm{3}} }{dt}\:{where}\:{t}\:=\:{u}−\mathrm{1}=\:\sqrt{{x}}−\mathrm{1} \\ $$$${v}=\mathrm{2}\left[\int\left(\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }\right){dt}\right]\:=\mathrm{2}\left(−\frac{\mathrm{1}}{{t}}+\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }\:+\:{c}\:\right) \\ $$$${v}\:=\:\mathrm{2}\left(−\frac{\mathrm{1}}{\:\sqrt{{x}}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:+\:{c}\right) \\ $$$${v}=\:\frac{\mathrm{3}−\mathrm{2}\sqrt{{x}}}{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:+\:{c} \\ $$
Commented by bemath last updated on 20/Jan/21
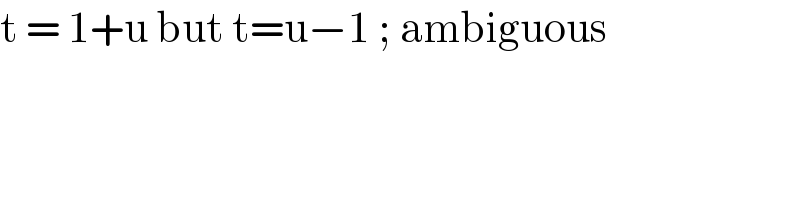
$$\mathrm{t}\:=\:\mathrm{1}+\mathrm{u}\:\mathrm{but}\:\mathrm{t}=\mathrm{u}−\mathrm{1}\:;\:\mathrm{ambiguous}\: \\ $$
