
Question Number 129825 by 0731619177 last updated on 19/Jan/21
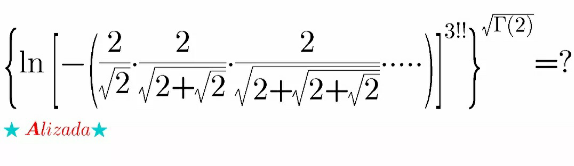
Answered by Olaf last updated on 20/Jan/21
![Let u_0 = 0 and u_n = (√(2+(√(2+(√(2...)))))), n ≥ 1 u_(n+1) = (√(2+u_n )) By induction : 0 ≤ u_n ≤ 2 ⇒ 0 ≤ u_(n+1) ≤ 2 So let u_n = 2cosθ_n (u_0 = 0 ⇒ θ_0 = (π/2)) u_(n+1) = (√(2+2cosθ_n )) = 2(√((1+cosθ_n )/2)) u_(n+1) = 2(√(cos^2 (θ_n /2))) = 2cos(θ_n /2) = 2cosθ_(n+1) ⇒ θ_(n+1) = (θ_n /2) Finally, θ_n = (θ_0 /2^n ) = (π/2^(n+1) ), u_n = 2cos(π/2^(n+1) ) sin2α = 2sinαcosα cosα = ((sin2α)/(2sinα)) ⇒ u_n = 2cosθ_n = ((sin2θ_n )/(sinθ_n )) = ((sin(π/2^n ))/(sin(π/2^(n+1) ))) Π_(n=1) ^N (2/u_n ) = 2^N Π_(n=1) ^N ((sin(π/2^(n+1) ))/(sin(π/2^n ))) = 2^N ((sin(π/2^(N+1) ))/(sin(π/2))) (telescopic product) Π_(n=1) ^N (2/u_n ) = 2^N sin(π/2^(N+1) ) ∼_∞ 2^N (π/2^(N+1) ) = (π/2) (1) 3!! = 6! = 720 (2) (√(Γ(2))) = (√(1!)) = 1 (3) With (1), (2) and (3) the result is : {ln[−((π/2))]^(720) }^1 = 720.ln(π/2)](Q129842.png)
$$\mathrm{Let}\:{u}_{\mathrm{0}} \:=\:\mathrm{0}\:\mathrm{and}\:{u}_{{n}} \:=\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}...}}},\:{n}\:\geqslant\:\mathrm{1} \\ $$$${u}_{{n}+\mathrm{1}} \:=\:\sqrt{\mathrm{2}+{u}_{{n}} } \\ $$$$\mathrm{By}\:\mathrm{induction}\:: \\ $$$$\mathrm{0}\:\leqslant\:{u}_{{n}} \:\leqslant\:\mathrm{2}\:\Rightarrow\:\mathrm{0}\:\leqslant\:{u}_{{n}+\mathrm{1}} \:\leqslant\:\mathrm{2} \\ $$$$\mathrm{So}\:\mathrm{let}\:{u}_{{n}} \:=\:\mathrm{2cos}\theta_{{n}} \:\left({u}_{\mathrm{0}} \:=\:\mathrm{0}\:\Rightarrow\:\theta_{\mathrm{0}} \:=\:\frac{\pi}{\mathrm{2}}\right) \\ $$$${u}_{{n}+\mathrm{1}} \:=\:\sqrt{\mathrm{2}+\mathrm{2cos}\theta_{{n}} }\:=\:\mathrm{2}\sqrt{\frac{\mathrm{1}+\mathrm{cos}\theta_{{n}} }{\mathrm{2}}} \\ $$$${u}_{{n}+\mathrm{1}} \:=\:\mathrm{2}\sqrt{\mathrm{cos}^{\mathrm{2}} \frac{\theta_{{n}} }{\mathrm{2}}}\:\:=\:\mathrm{2cos}\frac{\theta_{{n}} }{\mathrm{2}}\:=\:\mathrm{2cos}\theta_{{n}+\mathrm{1}} \\ $$$$\Rightarrow\:\theta_{{n}+\mathrm{1}} \:=\:\frac{\theta_{{n}} }{\mathrm{2}} \\ $$$$\mathrm{Finally},\:\theta_{{n}} \:=\:\frac{\theta_{\mathrm{0}} }{\mathrm{2}^{{n}} }\:=\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} },\:{u}_{{n}} \:=\:\mathrm{2cos}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$ \\ $$$$\mathrm{sin2}\alpha\:=\:\mathrm{2sin}\alpha\mathrm{cos}\alpha \\ $$$$\mathrm{cos}\alpha\:=\:\frac{\mathrm{sin2}\alpha}{\mathrm{2sin}\alpha} \\ $$$$\Rightarrow\:{u}_{{n}} \:=\:\mathrm{2cos}\theta_{{n}} =\:\frac{\mathrm{sin2}\theta_{{n}} }{\mathrm{sin}\theta_{{n}} }\:=\:\frac{\mathrm{sin}\frac{\pi}{\mathrm{2}^{{n}} }}{\mathrm{sin}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\prod}}\frac{\mathrm{2}}{{u}_{{n}} }\:=\:\mathrm{2}^{\mathrm{N}} \underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\prod}}\frac{\mathrm{sin}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }}{\mathrm{sin}\frac{\pi}{\mathrm{2}^{{n}} }}\:=\:\mathrm{2}^{\mathrm{N}} \frac{\mathrm{sin}\frac{\pi}{\mathrm{2}^{\mathrm{N}+\mathrm{1}} }}{\mathrm{sin}\frac{\pi}{\mathrm{2}}} \\ $$$$\left(\mathrm{telescopic}\:\mathrm{product}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\prod}}\frac{\mathrm{2}}{{u}_{{n}} }\:=\:\mathrm{2}^{\mathrm{N}} \mathrm{sin}\frac{\pi}{\mathrm{2}^{\mathrm{N}+\mathrm{1}} }\:\underset{\infty} {\sim}\:\mathrm{2}^{\mathrm{N}} \frac{\pi}{\mathrm{2}^{\mathrm{N}+\mathrm{1}} }\:=\:\frac{\pi}{\mathrm{2}}\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{3}!!\:=\:\mathrm{6}!\:=\:\mathrm{720}\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\sqrt{\Gamma\left(\mathrm{2}\right)}\:=\:\sqrt{\mathrm{1}!}\:=\:\mathrm{1}\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\mathrm{With}\:\left(\mathrm{1}\right),\:\left(\mathrm{2}\right)\:\mathrm{and}\:\left(\mathrm{3}\right)\:\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:: \\ $$$$\left\{\mathrm{ln}\left[−\left(\frac{\pi}{\mathrm{2}}\right)\right]^{\mathrm{720}} \right\}^{\mathrm{1}} \:=\:\mathrm{720}.\mathrm{ln}\frac{\pi}{\mathrm{2}} \\ $$
Commented by mr W last updated on 20/Jan/21

$$\mathrm{3}!!\neq\left(\mathrm{3}!\right)! \\ $$$$\mathrm{3}!!=\mathrm{3}×\mathrm{1}=\mathrm{3} \\ $$
Commented by Olaf last updated on 20/Jan/21

$$\mathrm{Sir},\:\mathrm{why}\:\mathrm{3}!!\:=\:\mathrm{3}×\mathrm{1}\:? \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{the}\:\mathrm{first}\:\mathrm{time}\:\mathrm{I}\:\mathrm{see}\:\mathrm{this}\:\mathrm{notation}. \\ $$
Commented by Olaf last updated on 20/Jan/21
$$\mathrm{Dear}\:\mathrm{mr}\:\mathrm{W},\:\mathrm{my}\:\mathrm{own}\:\mathrm{calculator} \\ $$$$\mathrm{gives}\::\:\mathrm{3}!!\:=\:\left(\mathrm{3}!\right)!\:=\:\mathrm{720} \\ $$
Commented by Olaf last updated on 20/Jan/21
Commented by mr W last updated on 20/Jan/21

