
Question Number 129807 by bramlexs22 last updated on 19/Jan/21
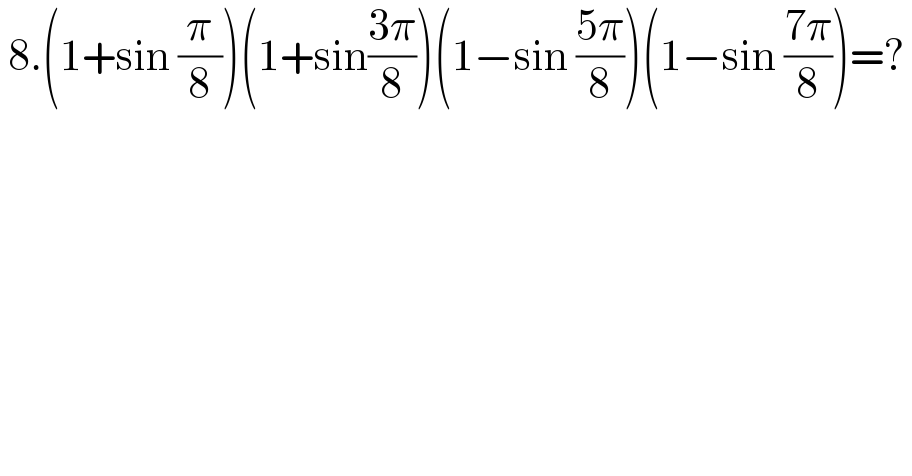
$$\:\mathrm{8}.\left(\mathrm{1}+\mathrm{sin}\:\frac{\pi}{\mathrm{8}}\right)\left(\mathrm{1}+\mathrm{sin}\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\left(\mathrm{1}−\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{8}}\right)\left(\mathrm{1}−\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{8}}\right)=?\: \\ $$
Answered by EDWIN88 last updated on 19/Jan/21
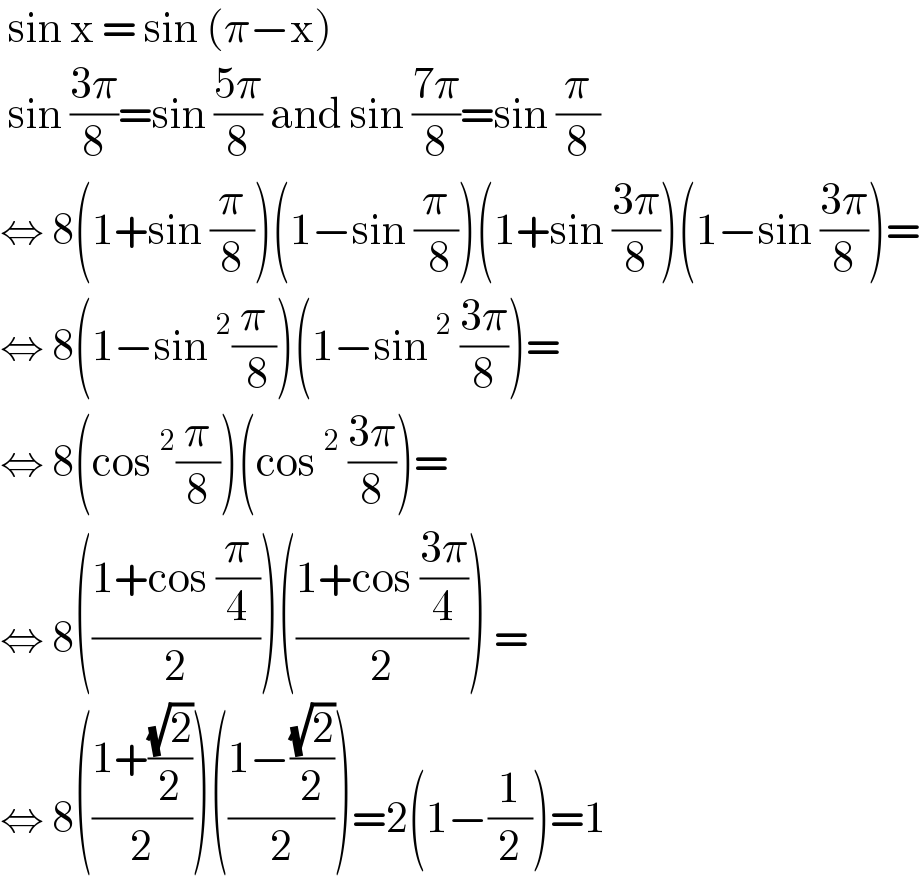
$$\:\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{sin}\:\left(\pi−\mathrm{x}\right) \\ $$$$\:\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{8}}=\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{8}}\:\mathrm{and}\:\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{8}}=\mathrm{sin}\:\frac{\pi}{\mathrm{8}} \\ $$$$\Leftrightarrow\:\mathrm{8}\left(\mathrm{1}+\mathrm{sin}\:\frac{\pi}{\mathrm{8}}\right)\left(\mathrm{1}−\mathrm{sin}\:\frac{\pi}{\:\mathrm{8}}\right)\left(\mathrm{1}+\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\left(\mathrm{1}−\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{8}}\right)= \\ $$$$\Leftrightarrow\:\mathrm{8}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \frac{\pi}{\:\mathrm{8}}\right)\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \:\frac{\mathrm{3}\pi}{\mathrm{8}}\right)= \\ $$$$\Leftrightarrow\:\mathrm{8}\left(\mathrm{cos}\:^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\right)\left(\mathrm{cos}\:^{\mathrm{2}} \:\frac{\mathrm{3}\pi}{\mathrm{8}}\right)= \\ $$$$\Leftrightarrow\:\mathrm{8}\left(\frac{\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{4}}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{4}}}{\mathrm{2}}\right)\:= \\ $$$$\Leftrightarrow\:\mathrm{8}\left(\frac{\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{2}}\right)=\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 19/Jan/21
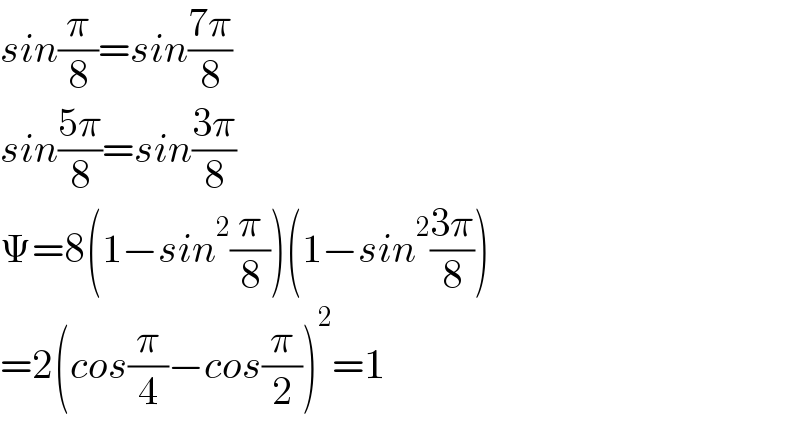
$${sin}\frac{\pi}{\mathrm{8}}={sin}\frac{\mathrm{7}\pi}{\mathrm{8}} \\ $$$${sin}\frac{\mathrm{5}\pi}{\mathrm{8}}={sin}\frac{\mathrm{3}\pi}{\mathrm{8}} \\ $$$$\Psi=\mathrm{8}\left(\mathrm{1}−{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\right)\left(\mathrm{1}−{sin}^{\mathrm{2}} \frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$$$=\mathrm{2}\left({cos}\frac{\pi}{\mathrm{4}}−{cos}\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$
