
Question Number 129674 by help last updated on 17/Jan/21

Commented by help last updated on 17/Jan/21

$$\mathrm{10}{b}? \\ $$
Answered by bemath last updated on 18/Jan/21
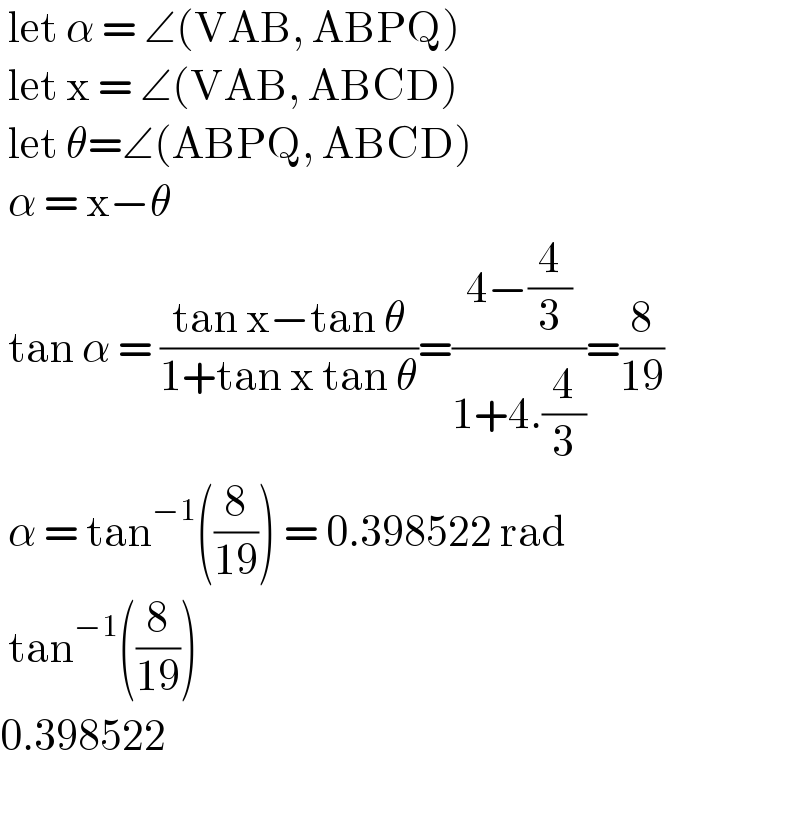
$$\:\mathrm{let}\:\alpha\:=\:\angle\left(\mathrm{VAB},\:\mathrm{ABPQ}\right) \\ $$$$\:\mathrm{let}\:\mathrm{x}\:=\:\angle\left(\mathrm{VAB},\:\mathrm{ABCD}\right) \\ $$$$\:\mathrm{let}\:\theta=\angle\left(\mathrm{ABPQ},\:\mathrm{ABCD}\right) \\ $$$$\:\alpha\:=\:\mathrm{x}−\theta \\ $$$$\:\mathrm{tan}\:\alpha\:=\:\frac{\mathrm{tan}\:\mathrm{x}−\mathrm{tan}\:\theta}{\mathrm{1}+\mathrm{tan}\:\mathrm{x}\:\mathrm{tan}\:\theta}=\frac{\mathrm{4}−\frac{\mathrm{4}}{\mathrm{3}}}{\mathrm{1}+\mathrm{4}.\frac{\mathrm{4}}{\mathrm{3}}}=\frac{\mathrm{8}}{\mathrm{19}} \\ $$$$\:\alpha\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{8}}{\mathrm{19}}\right)\:=\:\mathrm{0}.\mathrm{398522}\:\mathrm{rad} \\ $$$$\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{8}}{\mathrm{19}}\right) \\ $$$$\mathrm{0}.\mathrm{398522} \\ $$$$ \\ $$
