
Question Number 129672 by Dwaipayan Shikari last updated on 17/Jan/21

$$\int\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{97}} \right)^{\mathrm{7}} } \\ $$
Answered by mindispower last updated on 17/Jan/21

$${u}={x}^{\mathrm{97}} \Rightarrow{dx}=\frac{{u}^{−\frac{\mathrm{96}}{\mathrm{97}}} }{\mathrm{97}}{du} \\ $$$$=\int\frac{{u}^{−\frac{\mathrm{96}}{\mathrm{97}}} }{\mathrm{97}\left(\mathrm{1}+{u}\right)^{\mathrm{7}} }{du}...{E} \\ $$$$\int\frac{{x}^{{s}} }{\mathrm{1}+{x}}{dx}=\int\frac{{x}^{{s}} −{x}^{{s}+\mathrm{1}} }{\mathrm{1}−{x}^{\mathrm{2}} }{dx}...{F} \\ $$$${x}^{\mathrm{2}} ={t} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\mathrm{1}−{t}}\left({t}^{\mathrm{2}{s}−\frac{\mathrm{1}}{\mathrm{2}}} −{t}^{\mathrm{2}{s}+\frac{\mathrm{3}}{\mathrm{2}}} \right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}−{t}^{\mathrm{2}{s}+\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{1}−{t}}−\frac{\mathrm{1}−{t}^{\mathrm{2}{s}−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}−{t}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\Psi\left(\mathrm{2}{s}+\frac{\mathrm{5}}{\mathrm{2}}\right)−\Psi\left(\mathrm{2}{s}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$${iintegrate}\:{by}\:{part}\:\mathrm{6}\:{time}..{E\&F} \\ $$$${give}\:{us}\:{answr} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Jan/21
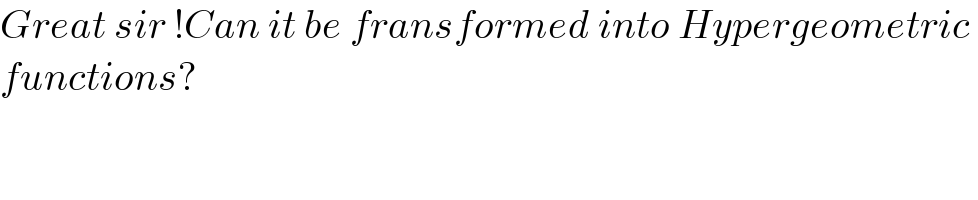
$${Great}\:{sir}\:!{Can}\:{it}\:{be}\:{fransformed}\:{into}\:{Hypergeometric}\: \\ $$$${functions}? \\ $$
Commented by mindispower last updated on 18/Jan/21
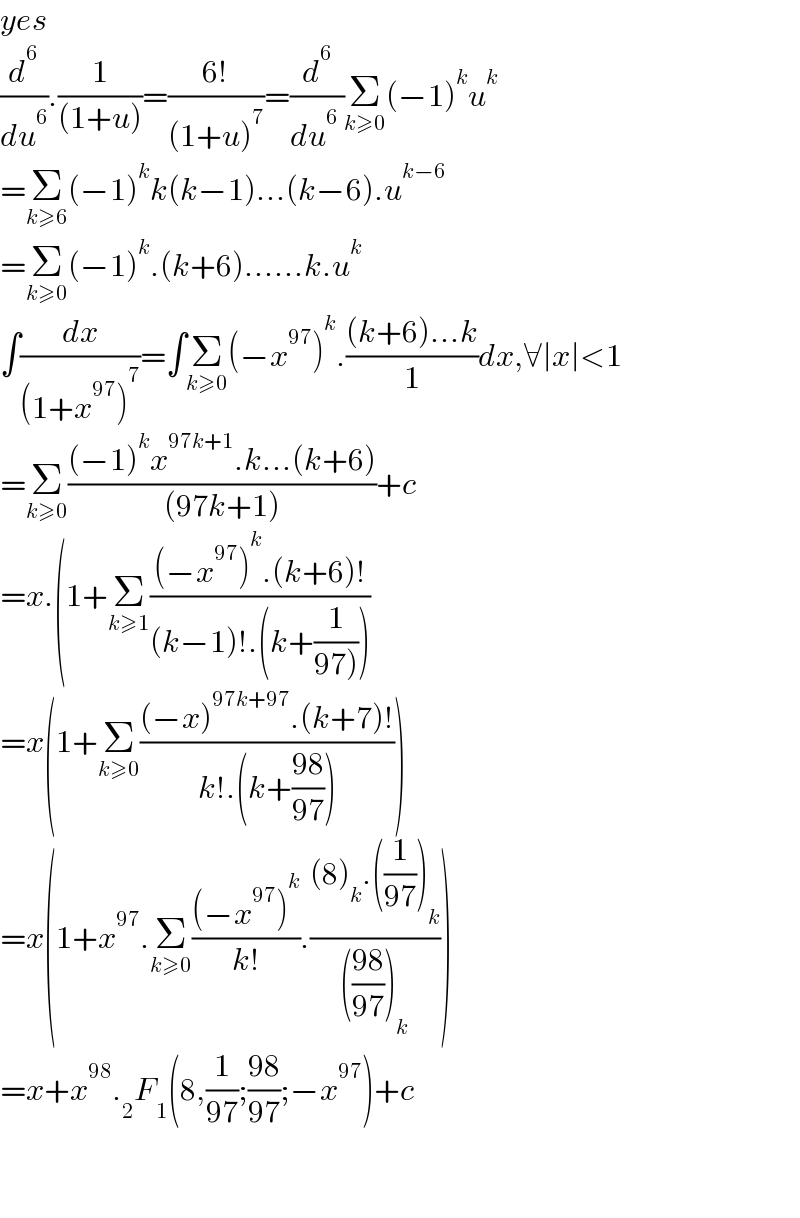
$${yes} \\ $$$$\frac{{d}^{\mathrm{6}} }{{du}^{\mathrm{6}} }.\frac{\mathrm{1}}{\left(\mathrm{1}+{u}\right)}=\frac{\mathrm{6}!}{\left(\mathrm{1}+{u}\right)^{\mathrm{7}} }=\frac{{d}^{\mathrm{6}} }{{du}^{\mathrm{6}} \:}\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} {u}^{{k}} \\ $$$$=\underset{{k}\geqslant\mathrm{6}} {\sum}\left(−\mathrm{1}\right)^{{k}} {k}\left({k}−\mathrm{1}\right)...\left({k}−\mathrm{6}\right).{u}^{{k}−\mathrm{6}} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} .\left({k}+\mathrm{6}\right)......{k}.{u}^{{k}} \\ $$$$\int\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{97}} \right)^{\mathrm{7}} }=\int\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−{x}^{\mathrm{97}} \right)^{{k}} .\frac{\left({k}+\mathrm{6}\right)...{k}}{\mathrm{1}}{dx},\forall\mid{x}\mid<\mathrm{1} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{97}{k}+\mathrm{1}} .{k}...\left({k}+\mathrm{6}\right)}{\left(\mathrm{97}{k}+\mathrm{1}\right)}+{c} \\ $$$$={x}.\left(\mathrm{1}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−{x}^{\mathrm{97}} \right)^{{k}} .\left({k}+\mathrm{6}\right)!}{\left({k}−\mathrm{1}\right)!.\left({k}+\frac{\mathrm{1}}{\left.\mathrm{97}\right)}\right)}\right. \\ $$$$={x}\left(\mathrm{1}+\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−{x}\right)^{\mathrm{97}{k}+\mathrm{97}} .\left({k}+\mathrm{7}\right)!}{{k}!.\left({k}+\frac{\mathrm{98}}{\mathrm{97}}\right)}\right) \\ $$$$={x}\left(\mathrm{1}+{x}^{\mathrm{97}} .\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−{x}^{\mathrm{97}} \right)^{{k}} }{{k}!}.\frac{\left(\mathrm{8}\right)_{{k}} .\left(\frac{\mathrm{1}}{\mathrm{97}}\right)_{{k}} }{\left(\frac{\mathrm{98}}{\mathrm{97}}\right)_{{k}} }\right) \\ $$$$={x}+{x}^{\mathrm{98}} ._{\mathrm{2}} {F}_{\mathrm{1}} \left(\mathrm{8},\frac{\mathrm{1}}{\mathrm{97}};\frac{\mathrm{98}}{\mathrm{97}};−{x}^{\mathrm{97}} \right)+{c} \\ $$$$ \\ $$$$ \\ $$
