
Previous in Differential Equation Next in Differential Equation
Question Number 129656 by Ahmed1hamouda last updated on 17/Jan/21
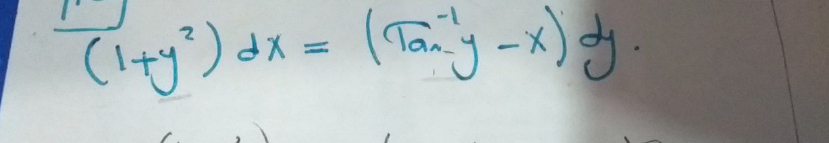
Commented by Ahmed1hamouda last updated on 17/Jan/21
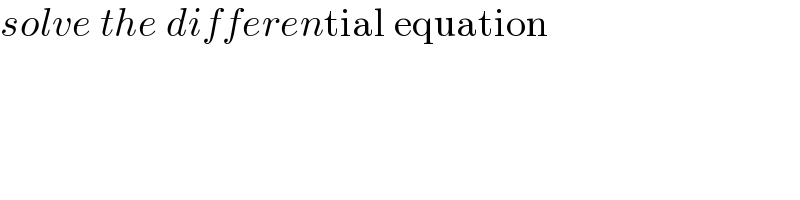
$${solve}\:{the}\:{differen}\mathrm{tial}\:\mathrm{equation} \\ $$
Answered by liberty last updated on 17/Jan/21
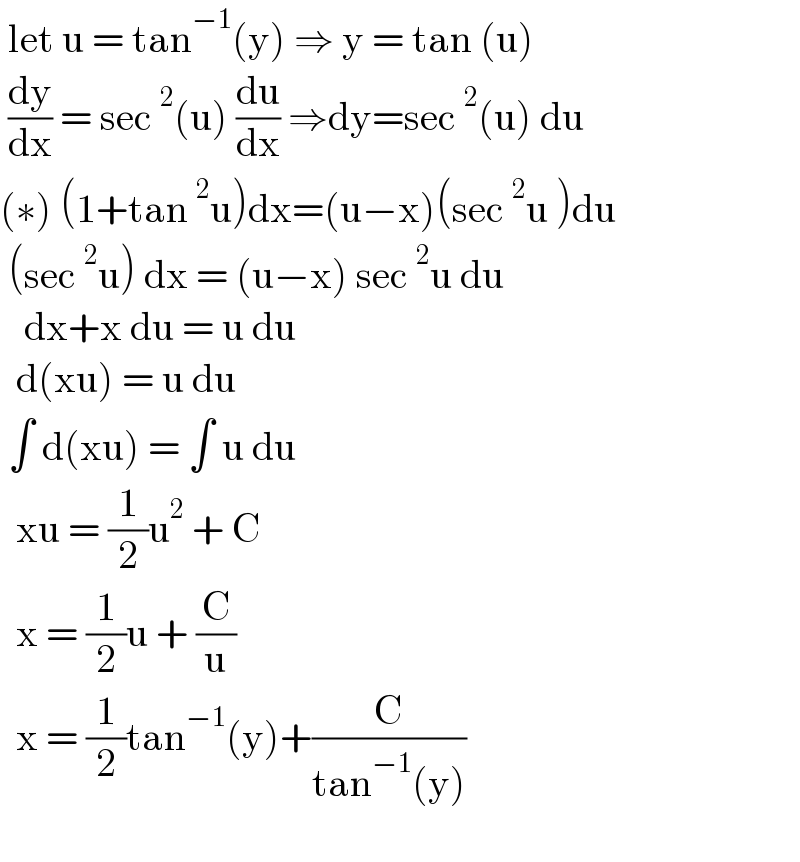
$$\:\mathrm{let}\:\mathrm{u}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{y}\right)\:\Rightarrow\:\mathrm{y}\:=\:\mathrm{tan}\:\left(\mathrm{u}\right) \\ $$$$\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{u}\right)\:\frac{\mathrm{du}}{\mathrm{dx}}\:\Rightarrow\mathrm{dy}=\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{u}\right)\:\mathrm{du} \\ $$$$\left(\ast\right)\:\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{u}\right)\mathrm{dx}=\left(\mathrm{u}−\mathrm{x}\right)\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}\:\right)\mathrm{du} \\ $$$$\:\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}\right)\:\mathrm{dx}\:=\:\left(\mathrm{u}−\mathrm{x}\right)\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}\:\mathrm{du}\: \\ $$$$\:\:\:\mathrm{dx}+\mathrm{x}\:\mathrm{du}\:=\:\mathrm{u}\:\mathrm{du}\: \\ $$$$\:\:\mathrm{d}\left(\mathrm{xu}\right)\:=\:\mathrm{u}\:\mathrm{du}\: \\ $$$$\:\int\:\mathrm{d}\left(\mathrm{xu}\right)\:=\:\int\:\mathrm{u}\:\mathrm{du}\: \\ $$$$\:\:\mathrm{xu}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}^{\mathrm{2}} \:+\:\mathrm{C}\: \\ $$$$\:\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}\:+\:\frac{\mathrm{C}}{\mathrm{u}} \\ $$$$\:\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{y}\right)+\frac{\mathrm{C}}{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{y}\right)} \\ $$$$ \\ $$
