
Question Number 129394 by liberty last updated on 15/Jan/21
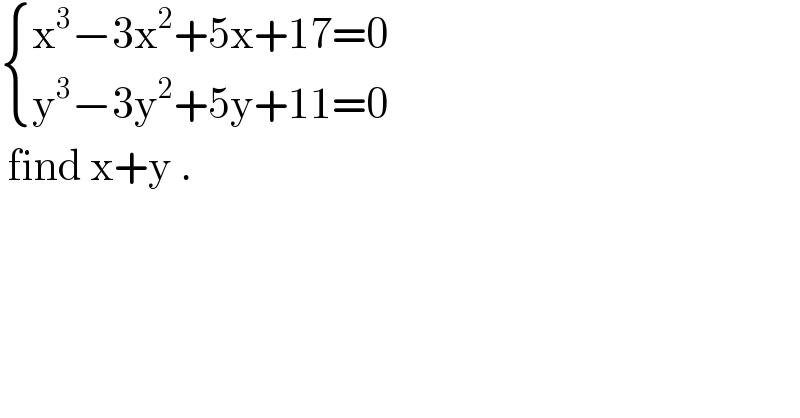
$$\begin{cases}{\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{5x}+\mathrm{17}=\mathrm{0}}\\{\mathrm{y}^{\mathrm{3}} −\mathrm{3y}^{\mathrm{2}} +\mathrm{5y}+\mathrm{11}=\mathrm{0}}\end{cases} \\ $$$$\:\mathrm{find}\:\mathrm{x}+\mathrm{y}\:. \\ $$
Answered by bemath last updated on 15/Jan/21
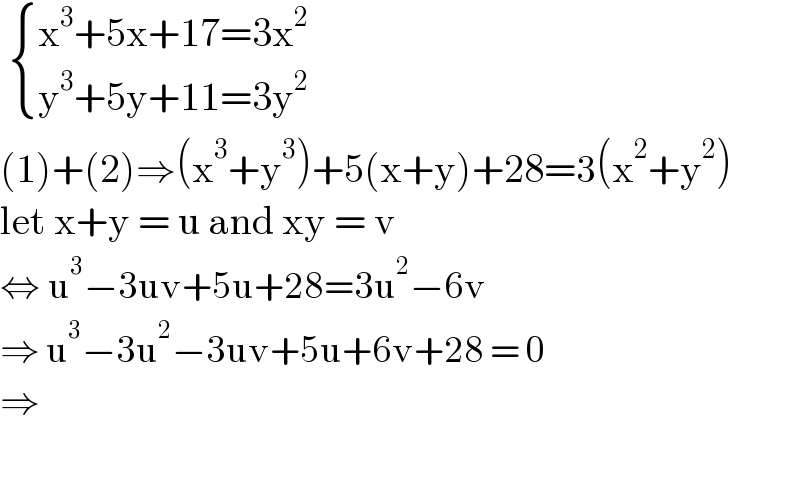
$$\:\begin{cases}{\mathrm{x}^{\mathrm{3}} +\mathrm{5x}+\mathrm{17}=\mathrm{3x}^{\mathrm{2}} }\\{\mathrm{y}^{\mathrm{3}} +\mathrm{5y}+\mathrm{11}=\mathrm{3y}^{\mathrm{2}} }\end{cases} \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\Rightarrow\left(\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} \right)+\mathrm{5}\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{28}=\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right) \\ $$$$\mathrm{let}\:\mathrm{x}+\mathrm{y}\:=\:\mathrm{u}\:\mathrm{and}\:\mathrm{xy}\:=\:\mathrm{v} \\ $$$$\Leftrightarrow\:\mathrm{u}^{\mathrm{3}} −\mathrm{3uv}+\mathrm{5u}+\mathrm{28}=\mathrm{3u}^{\mathrm{2}} −\mathrm{6v} \\ $$$$\Rightarrow\:\mathrm{u}^{\mathrm{3}} −\mathrm{3u}^{\mathrm{2}} −\mathrm{3uv}+\mathrm{5u}+\mathrm{6v}+\mathrm{28}\:=\:\mathrm{0} \\ $$$$\Rightarrow \\ $$$$ \\ $$
Answered by MJS_new last updated on 16/Jan/21

$${x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{17}=\mathrm{0} \\ $$$${x}={u}+\mathrm{1} \\ $$$${u}^{\mathrm{3}} +\mathrm{2}{u}+\mathrm{20}=\mathrm{0} \\ $$$${u}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{−\mathrm{10}+\frac{\mathrm{2}\sqrt{\mathrm{2031}}}{\mathrm{9}}}−\sqrt[{\mathrm{3}}]{\mathrm{10}+\frac{\mathrm{2}\sqrt{\mathrm{2031}}}{\mathrm{9}}} \\ $$$${u}_{\mathrm{2}} =\omega\sqrt[{\mathrm{3}}]{−\mathrm{10}+\frac{\mathrm{2}\sqrt{\mathrm{2031}}}{\mathrm{9}}}−\omega^{\mathrm{2}} \sqrt[{\mathrm{3}}]{\mathrm{10}+\frac{\mathrm{2}\sqrt{\mathrm{2031}}}{\mathrm{9}}} \\ $$$${u}_{\mathrm{3}} ={w}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{−\mathrm{10}+\frac{\mathrm{2}\sqrt{\mathrm{2031}}}{\mathrm{9}}}−\omega\sqrt[{\mathrm{3}}]{\mathrm{10}+\frac{\mathrm{2}\sqrt{\mathrm{2031}}}{\mathrm{9}}} \\ $$$$\mathrm{with}\:{w}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$ \\ $$$${y}^{\mathrm{3}} −\mathrm{3}{y}^{\mathrm{2}} +\mathrm{5}{y}+\mathrm{11}=\mathrm{0} \\ $$$${y}={v}+\mathrm{1} \\ $$$${v}^{\mathrm{3}} +\mathrm{2}{v}+\mathrm{14}=\mathrm{0} \\ $$$${v}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{−\mathrm{7}+\frac{\mathrm{11}\sqrt{\mathrm{33}}}{\mathrm{9}}}−\sqrt[{\mathrm{3}}]{\mathrm{7}+\frac{\mathrm{11}\sqrt{\mathrm{33}}}{\mathrm{9}}} \\ $$$${v}_{\mathrm{2}} =\omega\sqrt[{\mathrm{3}}]{−\mathrm{7}+\frac{\mathrm{11}\sqrt{\mathrm{33}}}{\mathrm{9}}}−\omega^{\mathrm{2}} \sqrt[{\mathrm{3}}]{\mathrm{7}+\frac{\mathrm{11}\sqrt{\mathrm{33}}}{\mathrm{9}}} \\ $$$${v}_{\mathrm{3}} =\omega^{\mathrm{2}} \sqrt[{\mathrm{3}}]{−\mathrm{7}+\frac{\mathrm{11}\sqrt{\mathrm{33}}}{\mathrm{9}}}−\omega\sqrt[{\mathrm{3}}]{\mathrm{7}+\frac{\mathrm{11}\sqrt{\mathrm{33}}}{\mathrm{9}}} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{adding}\:{x}\:\mathrm{and}\:{y}\:\mathrm{makes}\:\mathrm{any}\:\mathrm{sense}, \\ $$$$\mathrm{but}\:{x}_{\mathrm{1}} +{y}_{\mathrm{1}} = \\ $$$$=\mathrm{2}+\sqrt[{\mathrm{3}}]{−\mathrm{10}+\frac{\mathrm{2}\sqrt{\mathrm{2031}}}{\mathrm{9}}}−\sqrt[{\mathrm{3}}]{\mathrm{10}+\frac{\mathrm{2}\sqrt{\mathrm{2031}}}{\mathrm{9}}}+\sqrt[{\mathrm{3}}]{−\mathrm{7}+\frac{\mathrm{11}\sqrt{\mathrm{33}}}{\mathrm{9}}}−\sqrt[{\mathrm{3}}]{\mathrm{7}+\frac{\mathrm{11}\sqrt{\mathrm{33}}}{\mathrm{9}}} \\ $$$$\mathrm{with}\:\mathrm{no}\:\mathrm{chance}\:\mathrm{to}\:\mathrm{simplify} \\ $$
Answered by MJS_new last updated on 15/Jan/21
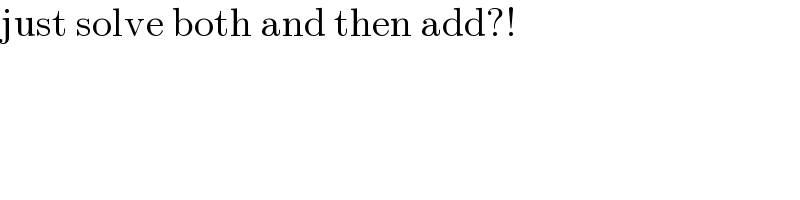
$$\mathrm{just}\:\mathrm{solve}\:\mathrm{both}\:\mathrm{and}\:\mathrm{then}\:\mathrm{add}?! \\ $$
Commented by MJS_new last updated on 16/Jan/21
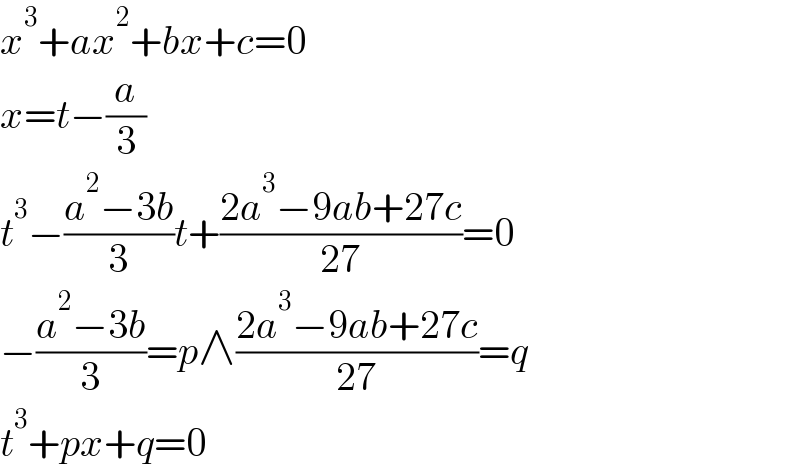
$${x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${x}={t}−\frac{{a}}{\mathrm{3}} \\ $$$${t}^{\mathrm{3}} −\frac{{a}^{\mathrm{2}} −\mathrm{3}{b}}{\mathrm{3}}{t}+\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{9}{ab}+\mathrm{27}{c}}{\mathrm{27}}=\mathrm{0} \\ $$$$−\frac{{a}^{\mathrm{2}} −\mathrm{3}{b}}{\mathrm{3}}={p}\wedge\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{9}{ab}+\mathrm{27}{c}}{\mathrm{27}}={q} \\ $$$${t}^{\mathrm{3}} +{px}+{q}=\mathrm{0} \\ $$
Commented by bemath last updated on 15/Jan/21

$$\mathrm{by}\:\mathrm{Cardano}? \\ $$
Commented by MJS_new last updated on 15/Jan/21

$$\mathrm{yes}.\:\mathrm{we}'\mathrm{ve}\:\mathrm{got}\:\mathrm{2}\:\mathrm{independent}\:\mathrm{equations}\:\mathrm{for} \\ $$$$\mathrm{2}\:\mathrm{independent}\:\mathrm{unknowns}...\:\mathrm{it}'\mathrm{s}\:\mathrm{like}\:\mathrm{adding} \\ $$$$\mathrm{your}\:\mathrm{height}\:\mathrm{to}\:\mathrm{your}\:\mathrm{weight}... \\ $$
Commented by bemath last updated on 15/Jan/21
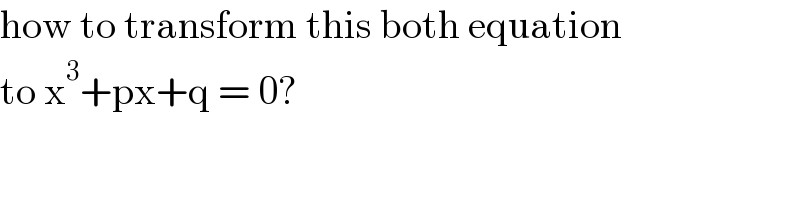
$$\mathrm{how}\:\mathrm{to}\:\mathrm{transform}\:\mathrm{this}\:\mathrm{both}\:\mathrm{equation}\: \\ $$$$\mathrm{to}\:\mathrm{x}^{\mathrm{3}} +\mathrm{px}+\mathrm{q}\:=\:\mathrm{0}? \\ $$
Commented by liberty last updated on 16/Jan/21
$$\mathrm{thank}\:\mathrm{you}.\:\mathrm{i}\:\mathrm{guess}\:\mathrm{the}\:\mathrm{question}\:\mathrm{any}\:\mathrm{mistake} \\ $$
