
Question Number 129308 by BHOOPENDRA last updated on 14/Jan/21
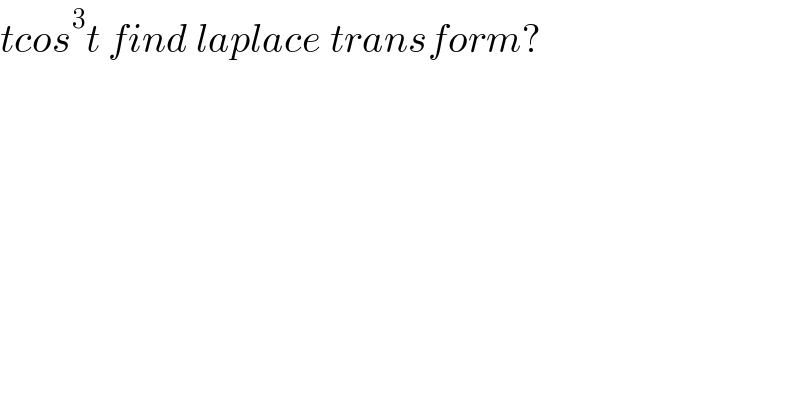
$${tcos}^{\mathrm{3}} {t}\:{find}\:{laplace}\:{transform}? \\ $$
Answered by Dwaipayan Shikari last updated on 14/Jan/21
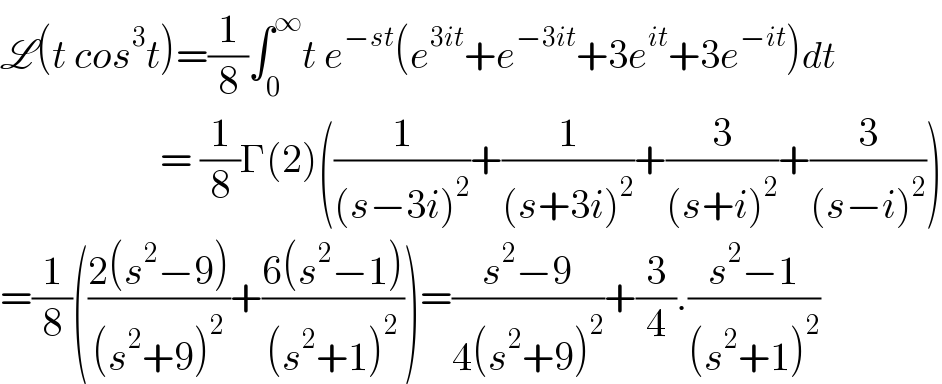
$$\mathscr{L}\left({t}\:{cos}^{\mathrm{3}} {t}\right)=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\infty} {t}\:{e}^{−{st}} \left({e}^{\mathrm{3}{it}} +{e}^{−\mathrm{3}{it}} +\mathrm{3}{e}^{{it}} +\mathrm{3}{e}^{−{it}} \right){dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{8}}\Gamma\left(\mathrm{2}\right)\left(\frac{\mathrm{1}}{\left({s}−\mathrm{3}{i}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({s}+\mathrm{3}{i}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\left({s}+{i}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\left({s}−{i}\right)^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{2}\left({s}^{\mathrm{2}} −\mathrm{9}\right)}{\left({s}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }+\frac{\mathrm{6}\left({s}^{\mathrm{2}} −\mathrm{1}\right)}{\left({s}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right)=\frac{{s}^{\mathrm{2}} −\mathrm{9}}{\mathrm{4}\left({s}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{4}}.\frac{{s}^{\mathrm{2}} −\mathrm{1}}{\left({s}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$
