
Previous in Differential Equation Next in Differential Equation
Question Number 129283 by math178 last updated on 14/Jan/21
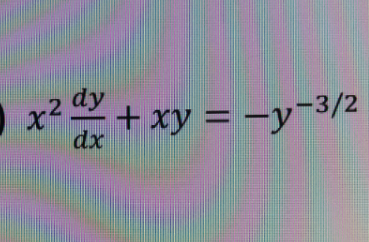
Commented by math178 last updated on 14/Jan/21
$${Bernoulli}\:{differential}\:{equations}\:{solution}\:? \\ $$$$ \\ $$
Answered by bramlexs22 last updated on 15/Jan/21

$$\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\frac{\mathrm{y}}{\mathrm{x}}\:=\:−\frac{\mathrm{y}^{−\mathrm{3}/\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{v}\:=\:\mathrm{y}^{\mathrm{1}−\left(−\mathrm{3}/\mathrm{2}\right)} =\mathrm{y}^{\mathrm{5}/\mathrm{2}} \\ $$$$\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\frac{\mathrm{5}}{\mathrm{2}}\mathrm{y}^{\mathrm{3}/\mathrm{2}} \:\frac{\mathrm{dy}}{\mathrm{dx}}\:\mathrm{or}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{2}}{\mathrm{5}}\mathrm{y}^{−\mathrm{3}/\mathrm{2}} \:\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\:\left(\ast\right)\:\frac{\mathrm{2}}{\mathrm{5}}\mathrm{y}^{−\mathrm{3}/\mathrm{2}} \:\frac{\mathrm{dv}}{\mathrm{dx}}\:+\:\frac{\mathrm{y}}{\mathrm{x}}\:=\:−\frac{\mathrm{y}^{−\mathrm{3}/\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{dv}}{\mathrm{dx}}\:+\:\frac{\mathrm{5}}{\mathrm{2}}\frac{\mathrm{v}}{\mathrm{x}}\:=\:−\frac{\mathrm{5}}{\mathrm{2x}^{\mathrm{2}} } \\ $$$$\:\mathrm{integrating}\:\mathrm{factor}\:\gamma\:=\:\mathrm{e}^{\int\:\frac{\mathrm{dx}}{\mathrm{x}}} =\:\mathrm{x} \\ $$$$\:\mathrm{v}\:=\:\frac{\int\:−\frac{\mathrm{5}}{\mathrm{2x}}\:\:+\:\mathrm{C}}{\:\mathrm{x}} \\ $$$$\:\mathrm{y}^{\mathrm{5}/\mathrm{2}} \:=\:\frac{−\frac{\mathrm{5}}{\mathrm{2}}\mathrm{ln}\:\mathrm{x}+\:\mathrm{C}}{\mathrm{x}} \\ $$$$\underline{\:\boldsymbol{\mathrm{y}}^{\mathrm{5}/\mathrm{2}} =−\frac{\mathrm{5}\boldsymbol{\mathrm{ln}}\:\boldsymbol{\mathrm{x}}}{\mathrm{2}\boldsymbol{\mathrm{x}}}\:+\:\boldsymbol{\mathrm{Cx}}^{−\mathrm{1}} \:.} \\ $$
