
Question Number 12928 by tawa last updated on 07/May/17
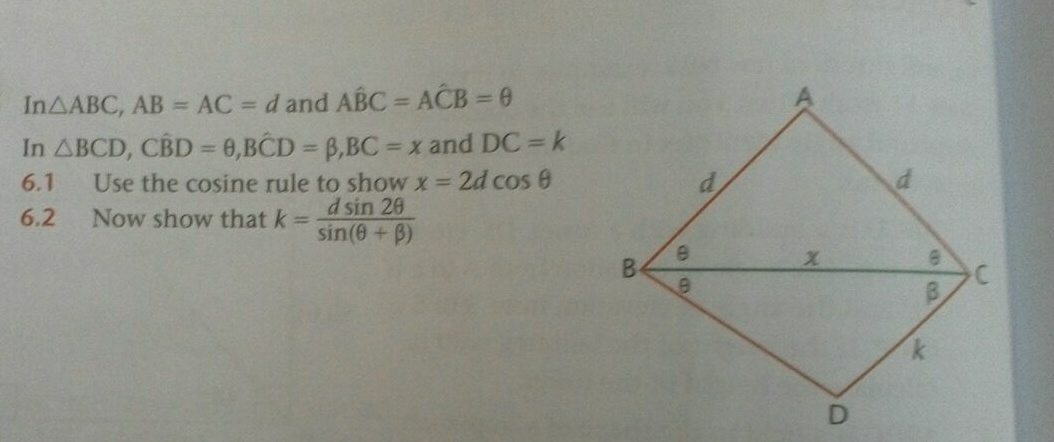
Answered by sandy_suhendra last updated on 09/May/17
![cosine rule in ΔABC : x^2 =d^2 +d^2 −2d.d.cos(180−2θ) x^2 =2d^2 −2d^2 (−cos2θ) ⇒ use cos2θ=2cos^2 θ−1 x^2 =2d^2 −2d^2 (−2cos^2 θ+1) x^2 =2d^2 +4d^2 cos^2 θ−2d^2 x^2 =4d^2 cos^2 θ x=2d cos θ sine rule in ΔBCD : (k/(sin θ)) = (x/(sin[180−(θ+β)])) (k/(sin θ)) = ((2d cos θ)/(sin(θ+β))) k = ((2d cos θ sin θ)/(sin(θ+β))) ⇒ use sin 2θ=2sinθcosθ k = ((2d(0.5 sin 2θ))/(sin(α+β))) k = ((d sin 2θ)/(sin(α+β)))](Q12992.png)
$$\mathrm{cosine}\:\mathrm{rule}\:\mathrm{in}\:\Delta\mathrm{ABC}\:: \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{d}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} −\mathrm{2d}.\mathrm{d}.\mathrm{cos}\left(\mathrm{180}−\mathrm{2}\theta\right) \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{2d}^{\mathrm{2}} −\mathrm{2d}^{\mathrm{2}} \left(−\mathrm{cos2}\theta\right)\:\Rightarrow\:\mathrm{use}\:\mathrm{cos2}\theta=\mathrm{2cos}^{\mathrm{2}} \theta−\mathrm{1}\:\:\:\:\: \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{2d}^{\mathrm{2}} −\mathrm{2d}^{\mathrm{2}} \left(−\mathrm{2cos}^{\mathrm{2}} \theta+\mathrm{1}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{2d}^{\mathrm{2}} +\mathrm{4d}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta−\mathrm{2d}^{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{4d}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta \\ $$$$\mathrm{x}=\mathrm{2d}\:\mathrm{cos}\:\theta \\ $$$$ \\ $$$$\mathrm{sine}\:\mathrm{rule}\:\mathrm{in}\:\Delta\mathrm{BCD}\:: \\ $$$$\frac{\mathrm{k}}{\mathrm{sin}\:\theta}\:=\:\frac{\mathrm{x}}{\mathrm{sin}\left[\mathrm{180}−\left(\theta+\beta\right)\right]} \\ $$$$\frac{\mathrm{k}}{\mathrm{sin}\:\theta}\:=\:\frac{\mathrm{2d}\:\mathrm{cos}\:\theta}{\mathrm{sin}\left(\theta+\beta\right)} \\ $$$$\mathrm{k}\:=\:\frac{\mathrm{2d}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta}{\mathrm{sin}\left(\theta+\beta\right)}\:\Rightarrow\:\mathrm{use}\:\mathrm{sin}\:\mathrm{2}\theta=\mathrm{2sin}\theta\mathrm{cos}\theta\:\:\:\:\: \\ $$$$\mathrm{k}\:=\:\frac{\mathrm{2d}\left(\mathrm{0}.\mathrm{5}\:\mathrm{sin}\:\mathrm{2}\theta\right)}{\mathrm{sin}\left(\alpha+\beta\right)} \\ $$$$\mathrm{k}\:=\:\frac{\mathrm{d}\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\left(\alpha+\beta\right)} \\ $$
