
Question Number 129244 by ajfour last updated on 14/Jan/21
Commented by ajfour last updated on 14/Jan/21

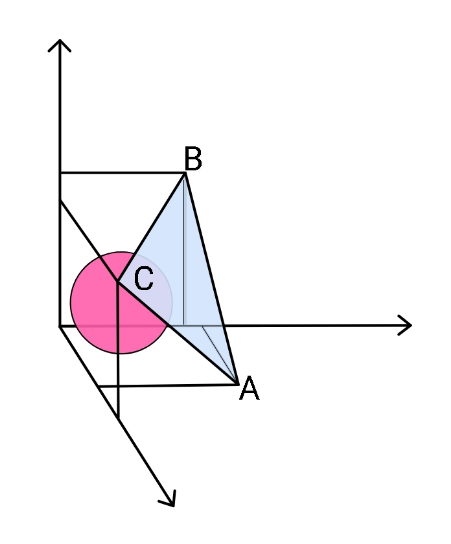
$${In}\:{terms}\:{of}\:{the}\:{sides}\:{of}\:\bigtriangleup{ABC}, \\ $$$${find}\:{largest}\:{radius}\:{sphere}\:{that} \\ $$$${can}\:{be}\:{placed}\:{against}\:{the}\:{room} \\ $$$${corner}\:{and}\:{triangle}.\:\:\:\:\: \\ $$
Answered by mr W last updated on 22/Feb/21
Commented by mr W last updated on 22/Feb/21
Commented by mr W last updated on 22/Feb/21
Commented by mr W last updated on 22/Feb/21

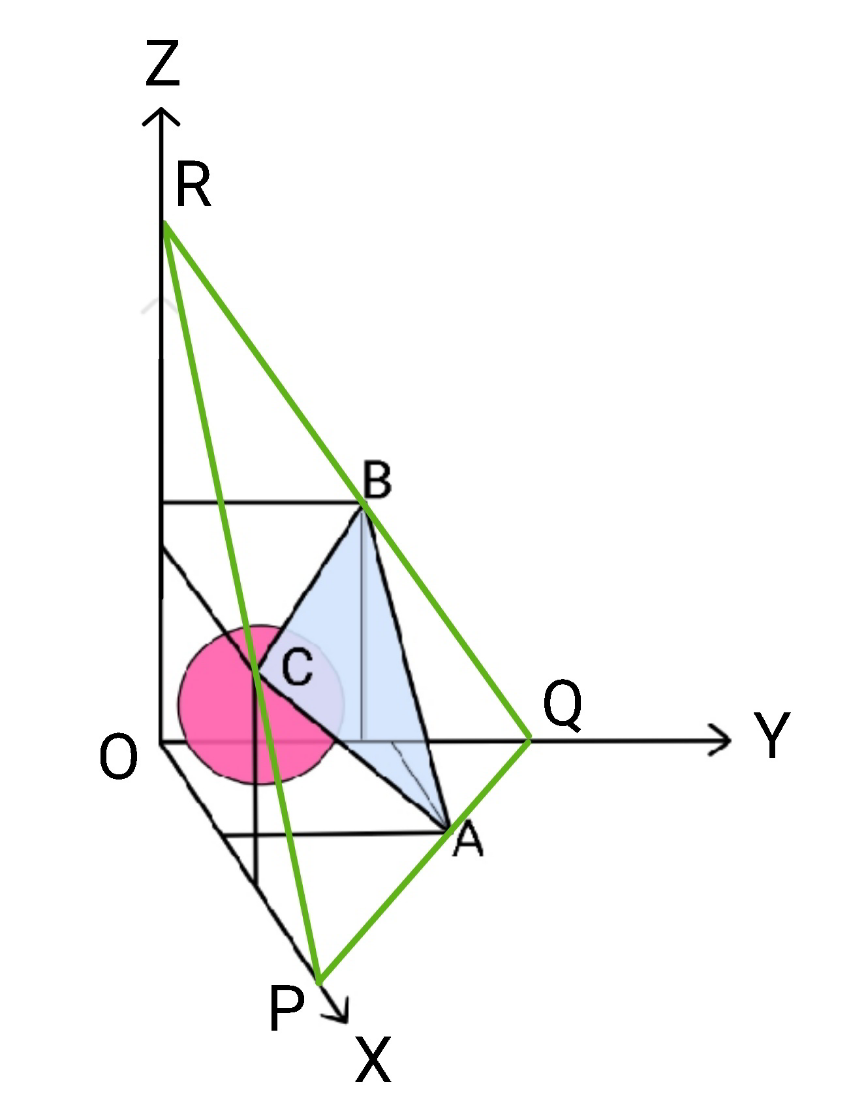
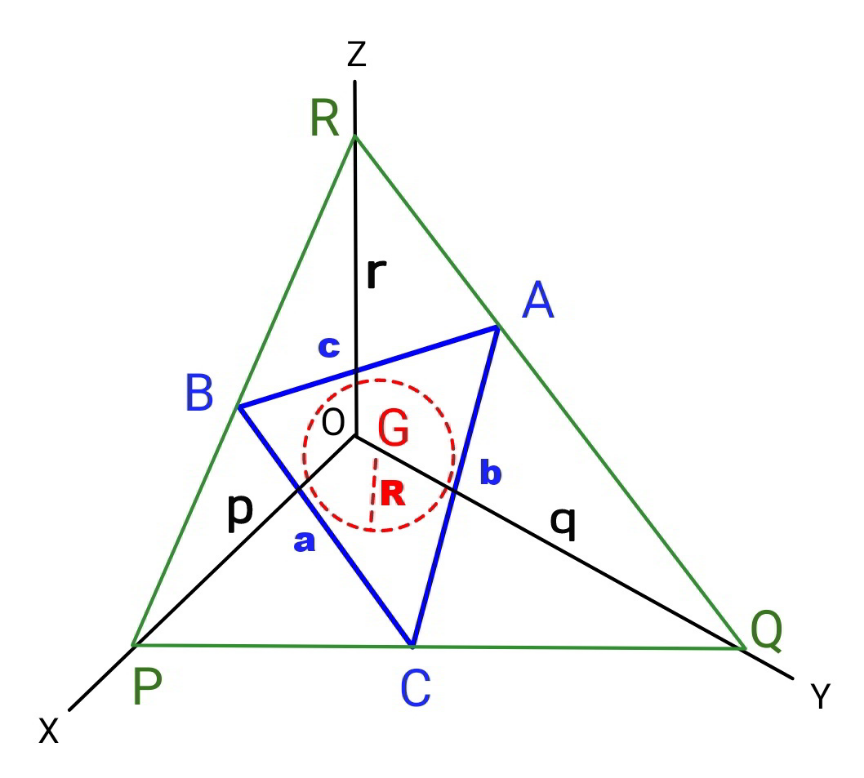
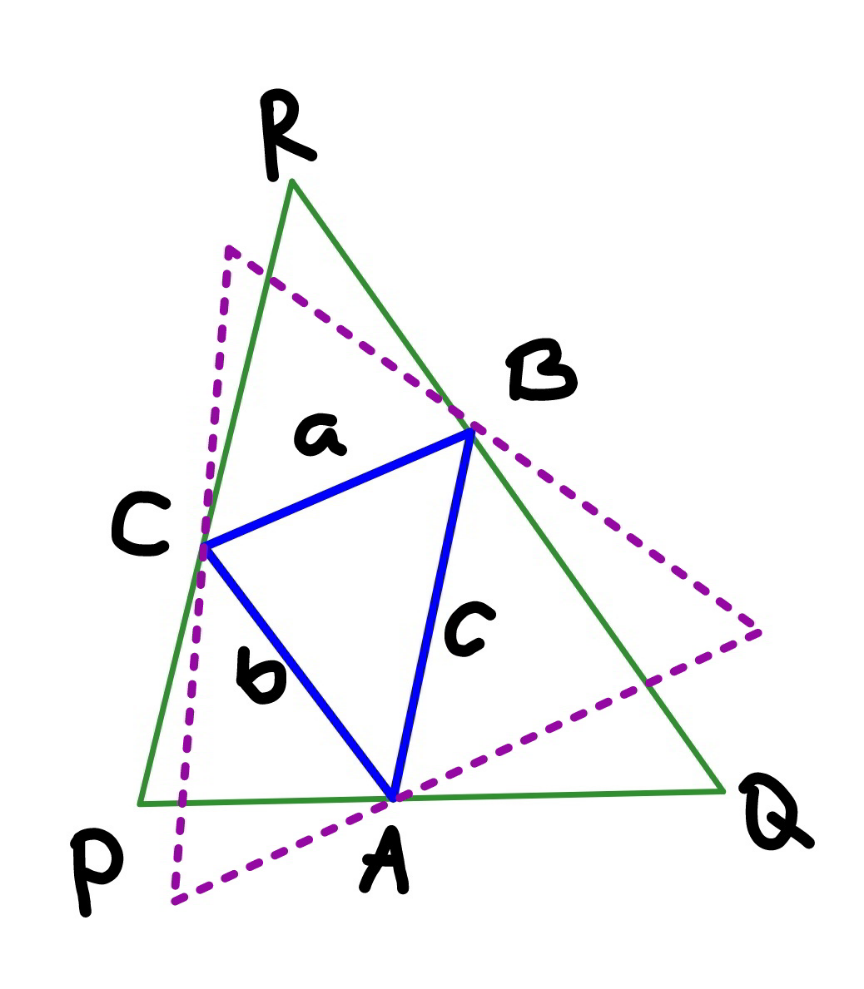
$${say}\:{the}\:{plane}\:{containing}\:{the}\:{triangle} \\ $$$${ABC}\:{intersects}\:{the}\:{coordinate}\:{axes} \\ $$$${at}\:{P},\:{Q},\:{R}. \\ $$$$\Delta{PQR}\:{is}\:{a}\:{circumtriangle}\:{of}\:{the} \\ $$$${given}\:{triangle}\:\Delta{ABC}. \\ $$$${say}\:{the}\:{sides}\:{of}\:\Delta{ABC}\:{are}\:{a},\:{b},\:{c}. \\ $$$${its}\:{area}\:{is}\:\Delta_{{ABC}} . \\ $$$$\Delta_{{ABC}} =\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$${with}\:{s}=\frac{{a}+{b}+{c}}{\mathrm{2}} \\ $$$$ \\ $$$${say}\:{the}\:{radius}\:{of}\:{the}\:{small}\:{sphere} \\ $$$${under}\:{the}\:{plane}\:{is}\:{R}\:{and}\: \\ $$$${its}\:{center}\:{is}\:{G}\left({R},{R},{R}\right).\:{the}\:{distance} \\ $$$${from}\:{G}\:{to}\:{the}\:{plane}\:\Delta{PQR}\:{is}\:{R}. \\ $$$$ \\ $$$${say}\:{P}\left({p},\mathrm{0},\mathrm{0}\right),\:{Q}\left(\mathrm{0},{q},\mathrm{0}\right),\:{R}\left(\mathrm{0},\mathrm{0},{r}\right). \\ $$$${the}\:{equation}\:{of}\:{the}\:{plane}\:{containing} \\ $$$$\Delta{ABC}\:{as}\:{well}\:{as}\:\Delta{PQR}\:{is} \\ $$$$\frac{{x}}{{p}}+\frac{{y}}{{q}}+\frac{{z}}{{r}}=\mathrm{1} \\ $$$${we}\:{have} \\ $$$${R}=\frac{\mid\frac{{R}}{{p}}+\frac{{R}}{{q}}+\frac{{R}}{{r}}−\mathrm{1}\mid}{\:\sqrt{\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }}}=\frac{\mathrm{1}−\left(\frac{{R}}{{p}}+\frac{{R}}{{q}}+\frac{{R}}{{r}}\right)}{\:\sqrt{\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }}} \\ $$$$\Rightarrow{R}=\frac{\mathrm{1}}{\frac{\mathrm{1}}{{p}}+\frac{\mathrm{1}}{{q}}+\frac{\mathrm{1}}{{r}}+\sqrt{\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }}} \\ $$$${due}\:{to}\:{symmetry}\:{of}\:{r}\:{w}.{r}.{t}.\:{p},{q},{r}\:{we} \\ $$$${know}\:{R}\:{is}\:{maximum}\:{when}\:{p}={q}={r}. \\ $$$$ \\ $$$${PQ}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} } \\ $$$${QR}=\sqrt{{q}^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$${RP}=\sqrt{{r}^{\mathrm{2}} +{p}^{\mathrm{2}} } \\ $$$${p}={q}={r}\:{means}\:{PQ}={QR}={RP},\:{i}.{e}. \\ $$$$\Delta{PQR}\:{is}\:{equilateral}. \\ $$$$ \\ $$$${the}\:{largest}\:{equilateral}\:{triangle}\:\Delta{PQR} \\ $$$${circumscribing}\:\Delta{ABC}\:{has}\:{side}\:{length} \\ $$$${PQ}={QR}={RP}={l}=\sqrt{\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}{\mathrm{3}}+\frac{\mathrm{8}\Delta_{{ABC}} }{\:\sqrt{\mathrm{3}}}} \\ $$$${with}\:\Delta_{{ABC}} ={area}\:{of}\:\Delta{ABC}. \\ $$$$\left({see}\:{Q}\mathrm{60313}\:{for}\:{more}\:{details}\right) \\ $$$${in}\:{this}\:{case}:\:{p}={q}={r}=\frac{{l}}{\:\sqrt{\mathrm{2}}} \\ $$$${R}_{{max}} =\frac{\mathrm{1}}{\frac{\mathrm{3}}{{p}}+\frac{\sqrt{\mathrm{3}}}{{p}}}=\frac{{p}}{\mathrm{3}+\sqrt{\mathrm{3}}}=\frac{{l}}{\left(\mathrm{3}+\sqrt{\mathrm{3}}\right)\sqrt{\mathrm{2}}} \\ $$$${R}_{{max}} =\frac{\mathrm{1}}{\left(\mathrm{3}+\sqrt{\mathrm{3}}\right)\sqrt{\mathrm{2}}}×\sqrt{\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}{\mathrm{3}}+\frac{\mathrm{8}\Delta_{{ABC}} }{\:\sqrt{\mathrm{3}}}} \\ $$$${R}_{{max}} =\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\Delta_{{ABC}} }}{\mathrm{3}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)} \\ $$$$ \\ $$$${btw},{for}\:{the}\:{big}\:{sphere}\:{over}\:{the}\:{plane} \\ $$$${containing}\:\Delta{ABC}\:{we}\:{have} \\ $$$${R}=\frac{\mid\frac{{R}}{{p}}+\frac{{R}}{{q}}+\frac{{R}}{{r}}−\mathrm{1}\mid}{\:\sqrt{\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }}}=\frac{\left(\frac{{R}}{{p}}+\frac{{R}}{{q}}+\frac{{R}}{{r}}\right)−\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }}} \\ $$$$\Rightarrow{R}_{{max}} =\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\Delta_{{ABC}} }}{\mathrm{3}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)} \\ $$
