
Question Number 129223 by bramlexs22 last updated on 14/Jan/21
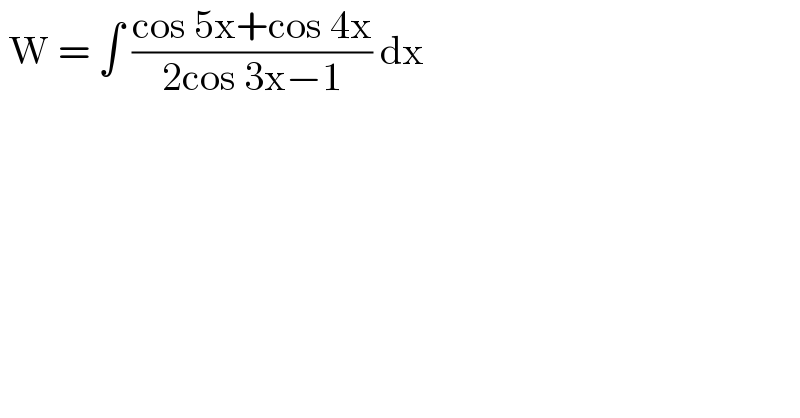
$$\:\mathrm{W}\:=\:\int\:\frac{\mathrm{cos}\:\mathrm{5x}+\mathrm{cos}\:\mathrm{4x}}{\mathrm{2cos}\:\mathrm{3x}−\mathrm{1}}\:\mathrm{dx}\: \\ $$
Answered by bobhans last updated on 14/Jan/21

$$\:{W}=\int\frac{\mathrm{2cos}\:\left(\frac{\mathrm{9}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2cos}\:\mathrm{3}{x}−\mathrm{1}}\:{dx} \\ $$$$\:{W}=\int\:\frac{\mathrm{2cos}\:\left(\frac{\mathrm{9}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right).\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{2cos}\:\mathrm{3}{x}\mathrm{sin}\:\mathrm{3}{x}−\mathrm{sin}\:\mathrm{3}{x}}\:{dx} \\ $$$$\:{W}=\:\int\:\frac{\mathrm{2cos}\:\left(\frac{\mathrm{9}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right)\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:\mathrm{6}{x}−\mathrm{sin}\:\mathrm{3}{x}}{dx} \\ $$$$\:{W}=\:\int\:\frac{\mathrm{2cos}\:\left(\frac{\mathrm{9}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right)\mathrm{2sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)}{−\mathrm{2cos}\:\left(\frac{\mathrm{9}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)}{dx} \\ $$$$\:{W}=−\int\:\mathrm{2sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right){dx} \\ $$$$\:{W}=\:−\int\:\left(\mathrm{sin}\:\mathrm{2}{x}+\mathrm{sin}\:{x}\right)\:{dx} \\ $$$$\underline{\:{W}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x}+\mathrm{cos}\:{x}\:+\:{C}\:} \\ $$
