
Question Number 129171 by benjo_mathlover last updated on 13/Jan/21
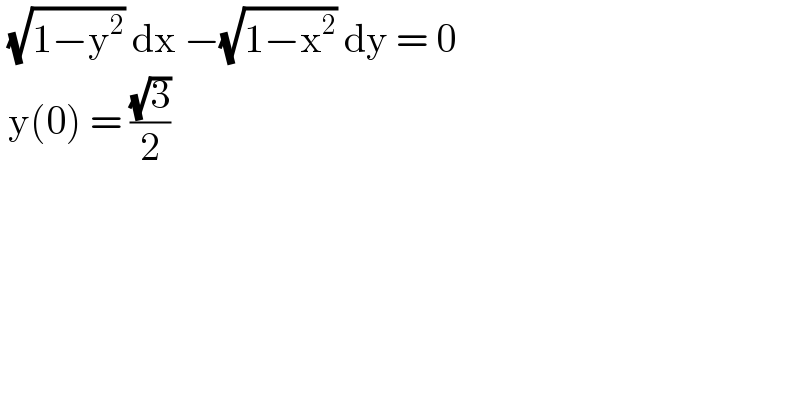
$$\:\sqrt{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }\:\mathrm{dx}\:−\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{dy}\:=\:\mathrm{0} \\ $$$$\:\mathrm{y}\left(\mathrm{0}\right)\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\: \\ $$
Answered by bramlexs22 last updated on 13/Jan/21
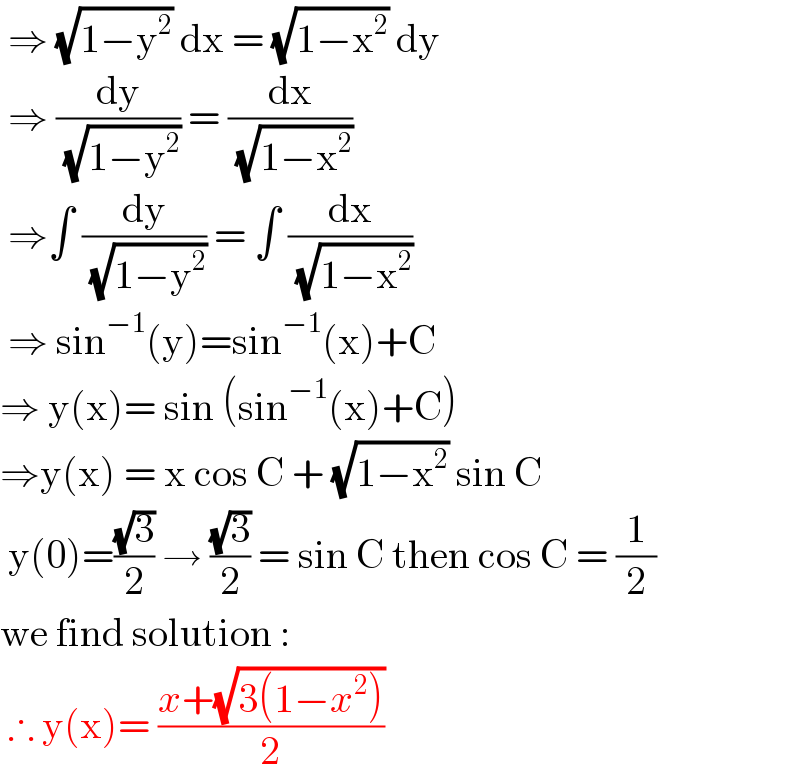
$$\:\Rightarrow\:\sqrt{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }\:\mathrm{dx}\:=\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{dy}\: \\ $$$$\:\Rightarrow\:\frac{\mathrm{dy}}{\:\sqrt{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }}\:=\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$\:\Rightarrow\int\:\frac{\mathrm{dy}}{\:\sqrt{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }}\:=\:\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\: \\ $$$$\:\Rightarrow\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{y}\right)=\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)+\mathrm{C} \\ $$$$\Rightarrow\:\mathrm{y}\left(\mathrm{x}\right)=\:\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)+\mathrm{C}\right) \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\:\mathrm{x}\:\mathrm{cos}\:\mathrm{C}\:+\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{sin}\:\mathrm{C} \\ $$$$\:\mathrm{y}\left(\mathrm{0}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\rightarrow\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:\mathrm{sin}\:\mathrm{C}\:\mathrm{then}\:\mathrm{cos}\:\mathrm{C}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{find}\:\mathrm{solution}\::\: \\ $$$$\:\therefore\:\mathrm{y}\left(\mathrm{x}\right)=\:\frac{{x}+\sqrt{\mathrm{3}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}}{\mathrm{2}}\: \\ $$
