
Previous in Differential Equation Next in Differential Equation
Question Number 129110 by math178 last updated on 12/Jan/21
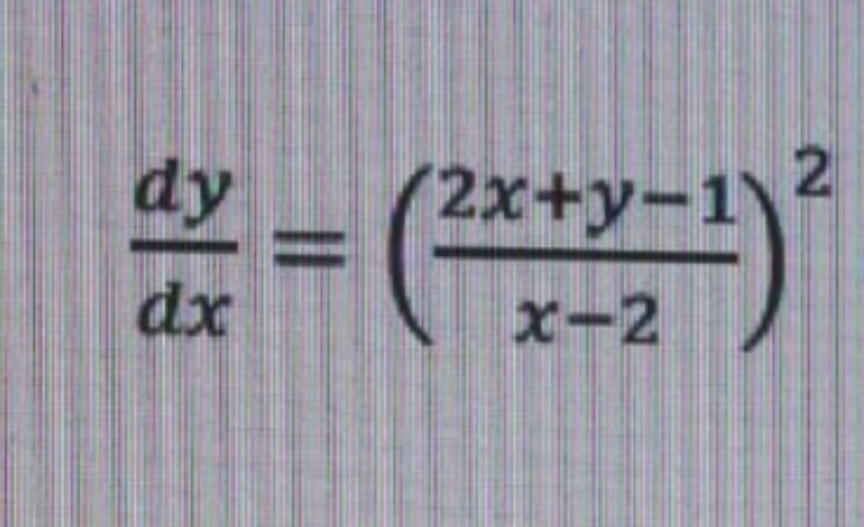
Commented by math178 last updated on 12/Jan/21

$${differential}\:{equation}\:{general}\:{solver}\:?\:{thank}\:{you} \\ $$
Answered by mr W last updated on 13/Jan/21
![u=((2x+y−1)/(x−2)) y=(x−2)u+1−2x y′=u+(x−2)u′−2=u^2 (x−2)u′=u^2 −u+2 (du/(u^2 −u+2))=(dx/(x−2)) (2/( (√7))) tan^(−1) ((2u−1)/( (√7)))=ln (x−2)+C u=((√7)/2) tan [((√7)/2)ln (x−2)+C]+(1/2) ⇒((2x+y−1)/(x−2))=((√7)/2) tan [((√7)/2)ln (x−2)+C]+(1/2)](Q129142.png)
$${u}=\frac{\mathrm{2}{x}+{y}−\mathrm{1}}{{x}−\mathrm{2}} \\ $$$${y}=\left({x}−\mathrm{2}\right){u}+\mathrm{1}−\mathrm{2}{x} \\ $$$${y}'={u}+\left({x}−\mathrm{2}\right){u}'−\mathrm{2}={u}^{\mathrm{2}} \\ $$$$\left({x}−\mathrm{2}\right){u}'={u}^{\mathrm{2}} −{u}+\mathrm{2} \\ $$$$\frac{{du}}{{u}^{\mathrm{2}} −{u}+\mathrm{2}}=\frac{{dx}}{{x}−\mathrm{2}} \\ $$$$\frac{\mathrm{2}}{\:\sqrt{\mathrm{7}}}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}{u}−\mathrm{1}}{\:\sqrt{\mathrm{7}}}=\mathrm{ln}\:\left({x}−\mathrm{2}\right)+{C} \\ $$$${u}=\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\:\mathrm{tan}\:\left[\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{ln}\:\left({x}−\mathrm{2}\right)+{C}\right]+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{2}{x}+{y}−\mathrm{1}}{{x}−\mathrm{2}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\:\mathrm{tan}\:\left[\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{ln}\:\left({x}−\mathrm{2}\right)+{C}\right]+\frac{\mathrm{1}}{\mathrm{2}} \\ $$
