
Question Number 129084 by mnjuly1970 last updated on 12/Jan/21
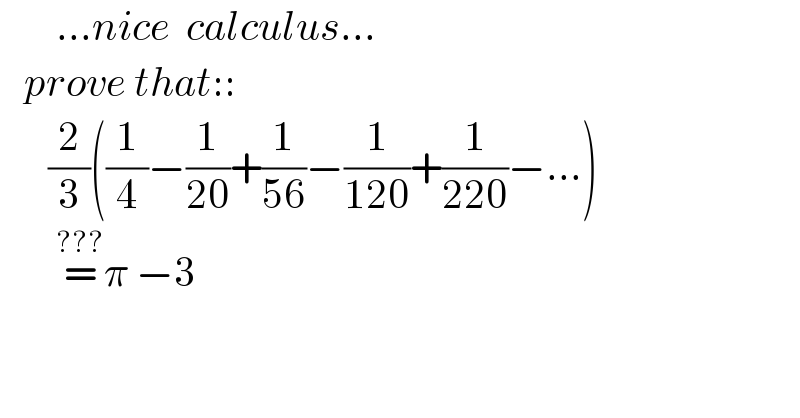
$$\:\:\:\:\:\:\:...{nice}\:\:{calculus}... \\ $$$$\:\:\:{prove}\:{that}:: \\ $$$$\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{20}}+\frac{\mathrm{1}}{\mathrm{56}}−\frac{\mathrm{1}}{\mathrm{120}}+\frac{\mathrm{1}}{\mathrm{220}}−...\right) \\ $$$$\:\:\:\:\:\:\:\overset{???} {=}\pi\:−\mathrm{3}\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 12/Jan/21
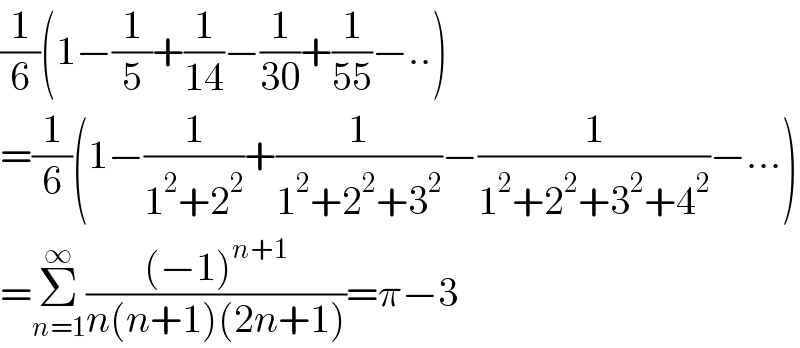
$$\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{14}}−\frac{\mathrm{1}}{\mathrm{30}}+\frac{\mathrm{1}}{\mathrm{55}}−..\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }−...\right) \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}=\pi−\mathrm{3} \\ $$
Commented by mnjuly1970 last updated on 12/Jan/21
$${excellent}\:\:{mr}\:{payan}\:. \\ $$$${thanks}\:{alot}... \\ $$
