
Question Number 129060 by benjo_mathlover last updated on 12/Jan/21
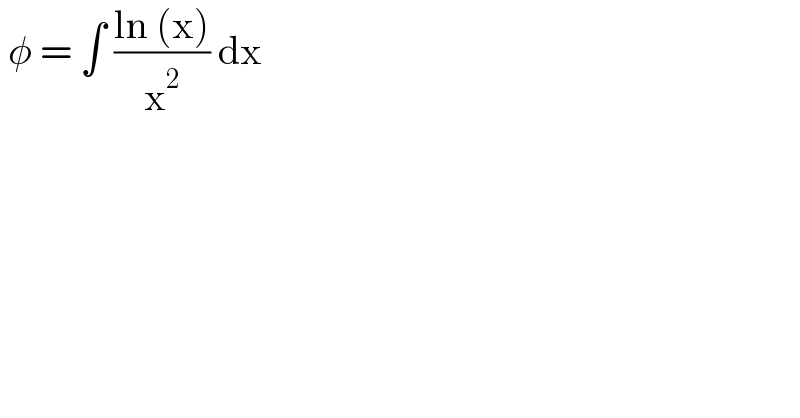
$$\:\phi\:=\:\int\:\frac{\mathrm{ln}\:\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\: \\ $$
Answered by liberty last updated on 12/Jan/21
![let ln (x)=h ⇒x = e^h φ = ∫ (h/e^(2h) ) (e^h dh )= ∫ h.e^(−h) dh ; [ by parts ] φ=−h.e^(−h) −e^(−h) + c φ = −((ln (x))/x)−(1/x) + c φ = ((−ln (x)−1)/x) + c](Q129062.png)
$$\:\mathrm{let}\:\mathrm{ln}\:\left(\mathrm{x}\right)=\mathrm{h}\:\Rightarrow\mathrm{x}\:=\:\mathrm{e}^{\mathrm{h}} \\ $$$$\:\phi\:=\:\int\:\frac{\mathrm{h}}{\mathrm{e}^{\mathrm{2h}} }\:\left(\mathrm{e}^{\mathrm{h}} \:\mathrm{dh}\:\right)=\:\int\:\mathrm{h}.\mathrm{e}^{−\mathrm{h}} \:\mathrm{dh}\:;\:\left[\:\mathrm{by}\:\mathrm{parts}\:\right] \\ $$$$\:\phi=−\mathrm{h}.\mathrm{e}^{−\mathrm{h}} −\mathrm{e}^{−\mathrm{h}} \:+\:\mathrm{c}\: \\ $$$$\:\phi\:=\:−\frac{\mathrm{ln}\:\left(\mathrm{x}\right)}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}}\:+\:\mathrm{c}\: \\ $$$$\:\phi\:=\:\frac{−\mathrm{ln}\:\left(\mathrm{x}\right)−\mathrm{1}}{\mathrm{x}}\:+\:\mathrm{c} \\ $$
