
Question Number 12905 by 433 last updated on 06/May/17
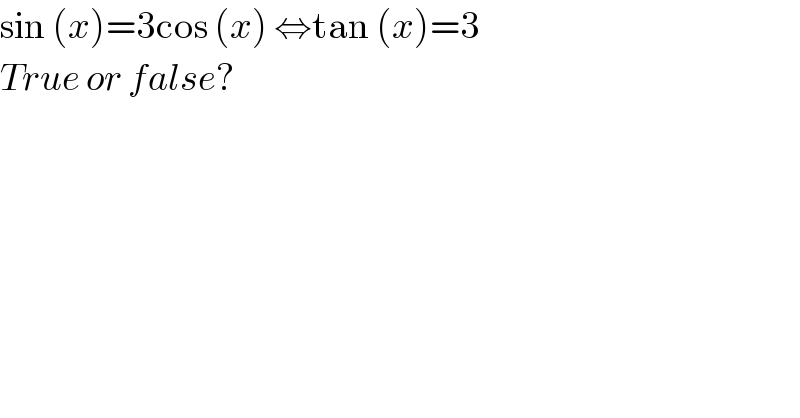
$$\mathrm{sin}\:\left({x}\right)=\mathrm{3cos}\:\left({x}\right)\:\Leftrightarrow\mathrm{tan}\:\left({x}\right)=\mathrm{3} \\ $$$${True}\:{or}\:{false}? \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 06/May/17
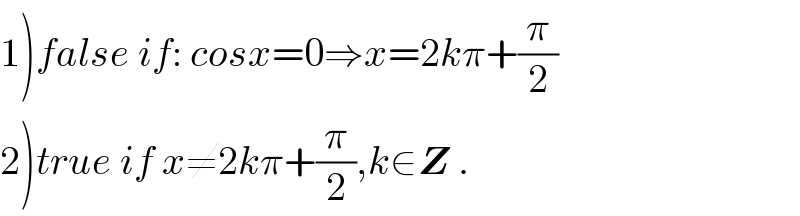
$$\left.\mathrm{1}\right){false}\:{if}:\:{cosx}=\mathrm{0}\Rightarrow{x}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right){true}\:{if}\:{x}\neq\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}},{k}\in\boldsymbol{{Z}}\:. \\ $$
Commented by mrW1 last updated on 07/May/17
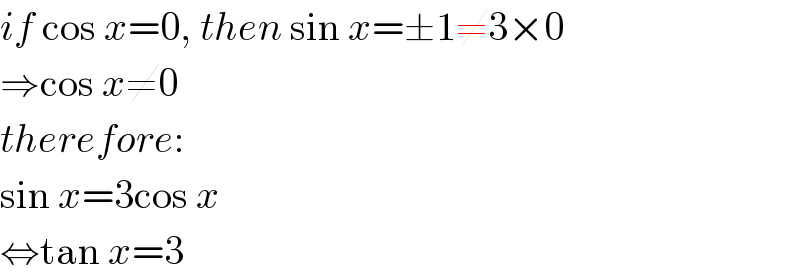
$${if}\:\mathrm{cos}\:{x}=\mathrm{0},\:{then}\:\mathrm{sin}\:{x}=\pm\mathrm{1}\neq\mathrm{3}×\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:{x}\neq\mathrm{0} \\ $$$${therefore}: \\ $$$$\mathrm{sin}\:{x}=\mathrm{3cos}\:{x} \\ $$$$\Leftrightarrow\mathrm{tan}\:{x}=\mathrm{3} \\ $$
Answered by mrW1 last updated on 07/May/17

$${true}! \\ $$
Commented by prakash jain last updated on 07/May/17
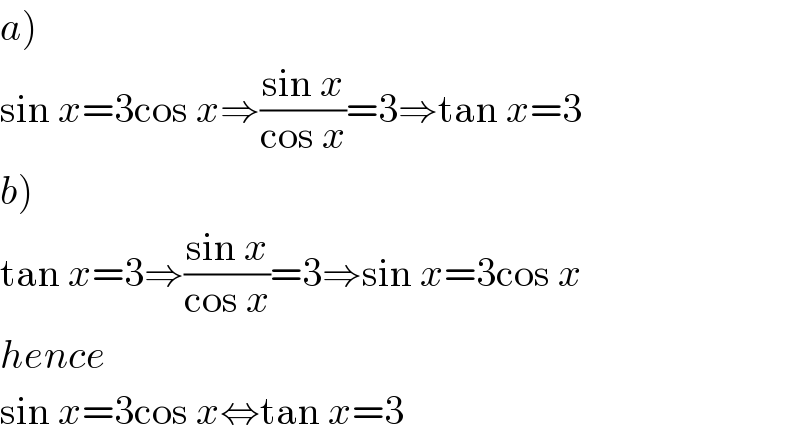
$$\left.{a}\right) \\ $$$$\mathrm{sin}\:{x}=\mathrm{3cos}\:{x}\Rightarrow\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}=\mathrm{3}\Rightarrow\mathrm{tan}\:{x}=\mathrm{3} \\ $$$$\left.{b}\right) \\ $$$$\mathrm{tan}\:{x}=\mathrm{3}\Rightarrow\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}=\mathrm{3}\Rightarrow\mathrm{sin}\:{x}=\mathrm{3cos}\:{x} \\ $$$${hence} \\ $$$$\mathrm{sin}\:{x}=\mathrm{3cos}\:{x}\Leftrightarrow\mathrm{tan}\:{x}=\mathrm{3} \\ $$
Commented by prakash jain last updated on 07/May/17
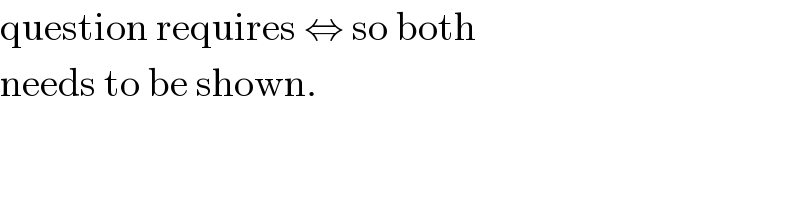
$$\mathrm{question}\:\mathrm{requires}\:\Leftrightarrow\:\mathrm{so}\:\mathrm{both} \\ $$$$\mathrm{needs}\:\mathrm{to}\:\mathrm{be}\:\mathrm{shown}.\: \\ $$
