
Question Number 129047 by Dwaipayan Shikari last updated on 12/Jan/21
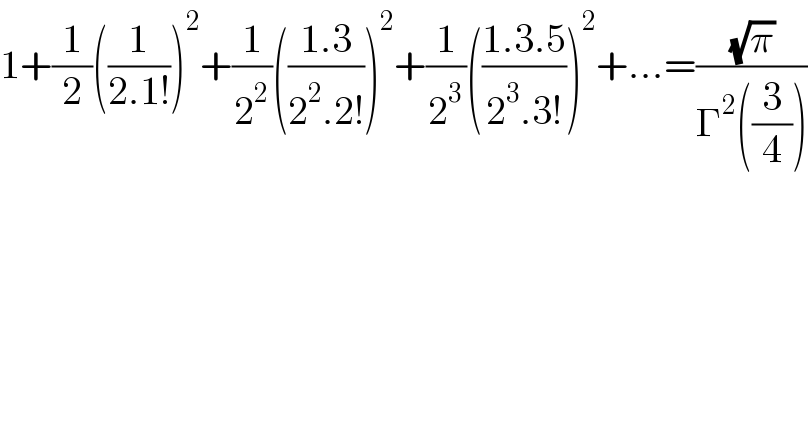
$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}.\mathrm{1}!}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\left(\frac{\mathrm{1}.\mathrm{3}}{\mathrm{2}^{\mathrm{2}} .\mathrm{2}!}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\left(\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}}{\mathrm{2}^{\mathrm{3}} .\mathrm{3}!}\right)^{\mathrm{2}} +...=\frac{\sqrt{\pi}}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$
Answered by mindispower last updated on 12/Jan/21
![1+Σ_(n≥1) (((Π_(k=0) ^(n−1) (1+2k))^2 )/(2^n (2^n .n!)^2 ))=S =1+Σ_(n≥1) ((2^(2n) Π_(k=0) ^(n−1) (k+(1/2))_n ^2 )/(2^n .2^(2n) .n!)).(1/(n!))=1+Σ_(k≥1) ((((1/2))_n ((1/2))_n )/((1)_n )).((((1/2))^n )/(n!)) =_2 F_1 ((1/2),(1/2);1;[(1/2)]) Baily′s theorem _2 F_1 (a,1−a;c;(1/2))=((Γ((c/2))Γ(((1+c)/2)))/(Γ(((c+a)/2))Γ(((c+1−a)/2)))) we get S=((Γ((1/2))Γ(1))/(Γ((3/4))Γ((3/4))))=((√π)/(Γ^2 ((3/4))))](Q129053.png)
$$\mathrm{1}+\underset{\boldsymbol{{n}}\geqslant\mathrm{1}} {\sum}\frac{\left(\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{1}+\mathrm{2}\boldsymbol{{k}}\right)\right)^{\mathrm{2}} }{\mathrm{2}^{{n}} \left(\mathrm{2}^{{n}} .{n}!\right)^{\mathrm{2}} }={S} \\ $$$$=\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{2}^{\mathrm{2}{n}} \underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} ^{\mathrm{2}} }{\mathrm{2}^{{n}} .\mathrm{2}^{\mathrm{2}{n}} .{n}!}.\frac{\mathrm{1}}{{n}!}=\mathrm{1}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{\left(\mathrm{1}\right)_{{n}} }.\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} }{{n}!} \\ $$$$=_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}};\mathrm{1};\left[\frac{\mathrm{1}}{\mathrm{2}}\right]\right) \\ $$$${Baily}'{s}\:{theorem}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left({a},\mathrm{1}−{a};{c};\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{{c}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}+{c}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{c}+{a}}{\mathrm{2}}\right)\Gamma\left(\frac{{c}+\mathrm{1}−{a}}{\mathrm{2}}\right)} \\ $$$${we}\:{get}\:{S}=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}\right)}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}=\frac{\sqrt{\pi}}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$
Commented by Dwaipayan Shikari last updated on 12/Jan/21
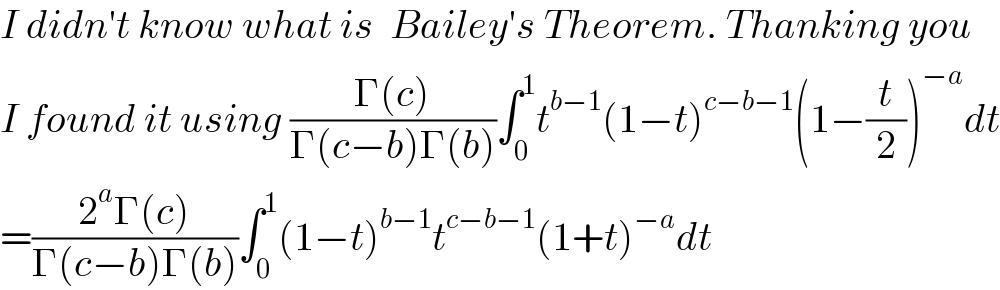
$${I}\:{didn}'{t}\:{know}\:{what}\:{is}\:\:{Bailey}'{s}\:{Theorem}.\:{Thanking}\:{you}\: \\ $$$${I}\:{found}\:{it}\:{using}\:\frac{\Gamma\left({c}\right)}{\Gamma\left({c}−{b}\right)\Gamma\left({b}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{b}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{c}−{b}−\mathrm{1}} \left(\mathrm{1}−\frac{{t}}{\mathrm{2}}\right)^{−{a}} {dt} \\ $$$$=\frac{\mathrm{2}^{{a}} \Gamma\left({c}\right)}{\Gamma\left({c}−{b}\right)\Gamma\left({b}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{b}−\mathrm{1}} {t}^{{c}−{b}−\mathrm{1}} \left(\mathrm{1}+{t}\right)^{−{a}} {dt}\:\:\: \\ $$
Commented by mindispower last updated on 12/Jan/21

$${yes}\:{symetrie}\:{x},\mathrm{1}−{x}, \\ $$
