
Question Number 128908 by bramlexs22 last updated on 11/Jan/21
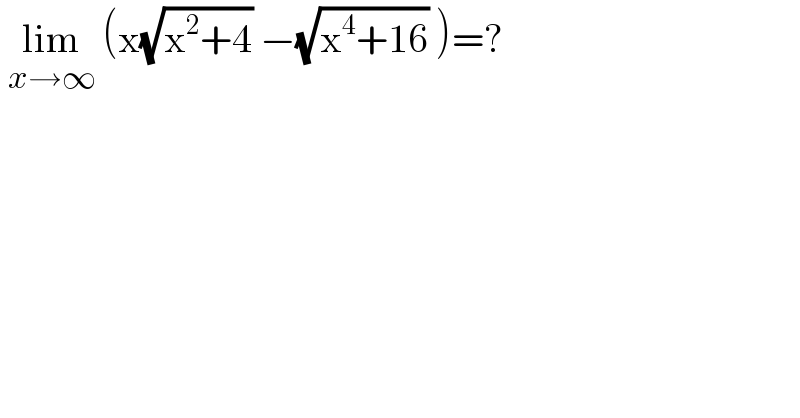
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}\:−\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{16}}\:\right)=? \\ $$
Answered by Dwaipayan Shikari last updated on 11/Jan/21
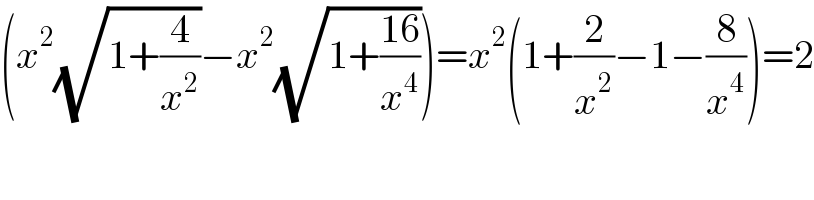
$$\left({x}^{\mathrm{2}} \sqrt{\mathrm{1}+\frac{\mathrm{4}}{{x}^{\mathrm{2}} }}−{x}^{\mathrm{2}} \sqrt{\mathrm{1}+\frac{\mathrm{16}}{{x}^{\mathrm{4}} }}\right)={x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }−\mathrm{1}−\frac{\mathrm{8}}{{x}^{\mathrm{4}} }\right)=\mathrm{2} \\ $$
Answered by liberty last updated on 11/Jan/21
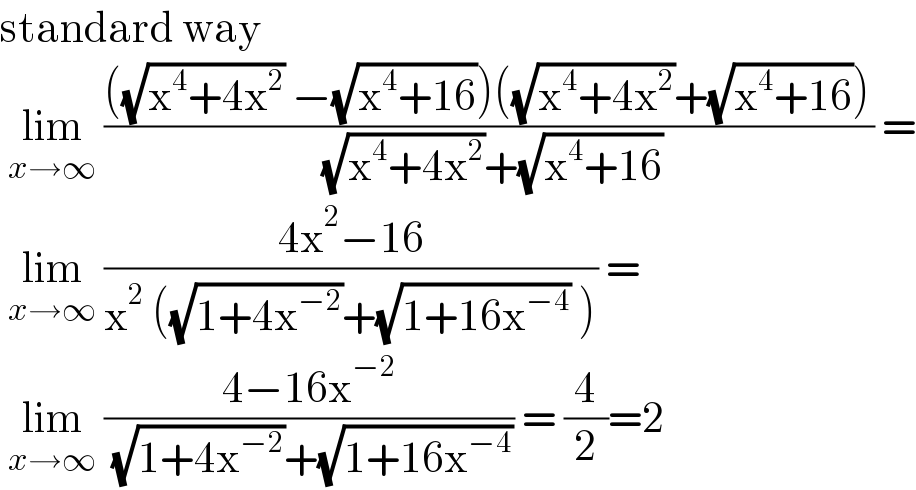
$$\mathrm{standard}\:\mathrm{way}\: \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{2}} }\:−\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{16}}\right)\left(\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{2}} }+\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{16}}\right)}{\:\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{2}} }+\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{16}}}\:= \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{4x}^{\mathrm{2}} −\mathrm{16}}{\mathrm{x}^{\mathrm{2}} \:\left(\sqrt{\mathrm{1}+\mathrm{4x}^{−\mathrm{2}} }+\sqrt{\mathrm{1}+\mathrm{16x}^{−\mathrm{4}} }\:\right)}\:=\: \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{4}−\mathrm{16x}^{−\mathrm{2}} }{\:\sqrt{\mathrm{1}+\mathrm{4x}^{−\mathrm{2}} }+\sqrt{\mathrm{1}+\mathrm{16x}^{−\mathrm{4}} }}\:=\:\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$
