
Question Number 128907 by bramlexs22 last updated on 11/Jan/21
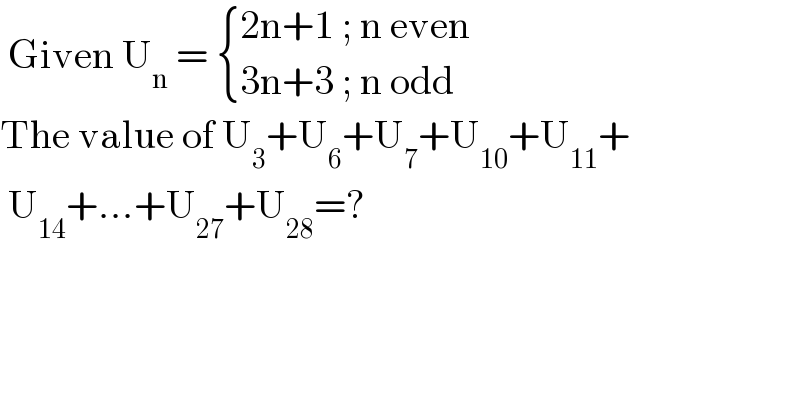
$$\:\mathrm{Given}\:\mathrm{U}_{\mathrm{n}} \:=\:\begin{cases}{\mathrm{2n}+\mathrm{1}\:;\:\mathrm{n}\:\mathrm{even}}\\{\mathrm{3n}+\mathrm{3}\:;\:\mathrm{n}\:\mathrm{odd}}\end{cases} \\ $$$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\mathrm{U}_{\mathrm{3}} +\mathrm{U}_{\mathrm{6}} +\mathrm{U}_{\mathrm{7}} +\mathrm{U}_{\mathrm{10}} +\mathrm{U}_{\mathrm{11}} + \\ $$$$\:\mathrm{U}_{\mathrm{14}} +...+\mathrm{U}_{\mathrm{27}} +\mathrm{U}_{\mathrm{28}} =? \\ $$
Answered by Olaf last updated on 11/Jan/21
![S = Σ_(k=3) ^(k=28) U_k S = Σ_(n=1) ^(n=13) [U_(2n+1) +U_(2n+2) ] S = Σ_(n=1) ^(n=13) [(3(2n+1)+3)+(2(2n+2)+1)] S = Σ_(n=1) ^(n=13) (10n+11) S = 10((13×14)/2)+11×13 = 910+143 = 1053](Q128919.png)
$$ \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{3}} {\overset{{k}=\mathrm{28}} {\sum}}\mathrm{U}_{{k}} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{{n}=\mathrm{13}} {\sum}}\left[\mathrm{U}_{\mathrm{2}{n}+\mathrm{1}} +\mathrm{U}_{\mathrm{2}{n}+\mathrm{2}} \right] \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{{n}=\mathrm{13}} {\sum}}\left[\left(\mathrm{3}\left(\mathrm{2}{n}+\mathrm{1}\right)+\mathrm{3}\right)+\left(\mathrm{2}\left(\mathrm{2}{n}+\mathrm{2}\right)+\mathrm{1}\right)\right] \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{{n}=\mathrm{13}} {\sum}}\left(\mathrm{10}{n}+\mathrm{11}\right) \\ $$$$\mathrm{S}\:=\:\mathrm{10}\frac{\mathrm{13}×\mathrm{14}}{\mathrm{2}}+\mathrm{11}×\mathrm{13}\:=\:\mathrm{910}+\mathrm{143}\:=\:\mathrm{1053} \\ $$
