
Question Number 128850 by ruwedkabeh last updated on 10/Jan/21
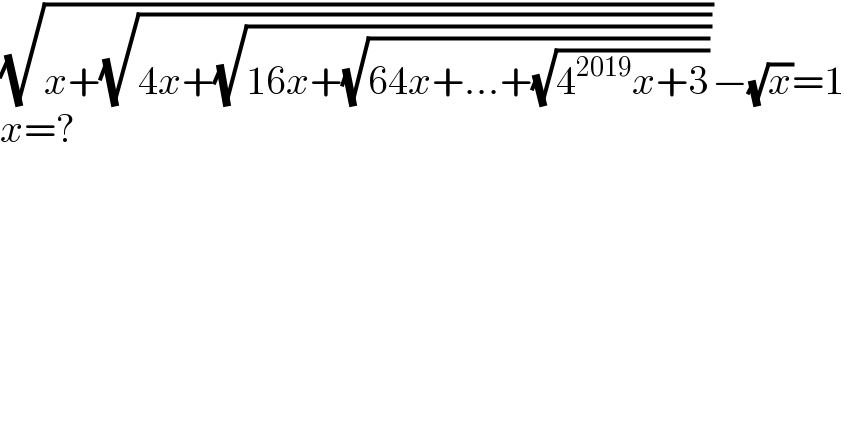
$$\sqrt{{x}+\sqrt{\mathrm{4}{x}+\sqrt{\mathrm{16}{x}+\sqrt{\mathrm{64}{x}+...+\sqrt{\mathrm{4}^{\mathrm{2019}} {x}+\mathrm{3}}}}}}−\sqrt{{x}}=\mathrm{1} \\ $$$${x}=? \\ $$
Answered by mindispower last updated on 10/Jan/21
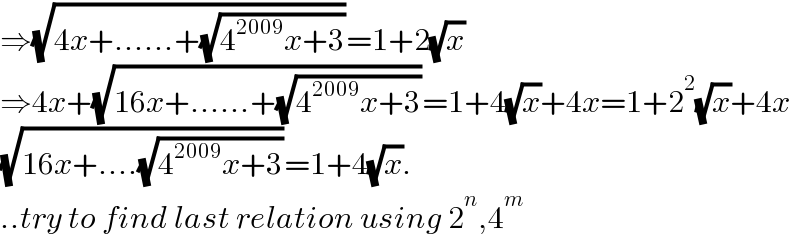
$$\Rightarrow\sqrt{\mathrm{4}{x}+......+\sqrt{\mathrm{4}^{\mathrm{2009}} {x}+\mathrm{3}}}=\mathrm{1}+\mathrm{2}\sqrt{{x}} \\ $$$$\Rightarrow\mathrm{4}{x}+\sqrt{\mathrm{16}{x}+......+\sqrt{\mathrm{4}^{\mathrm{2009}} {x}+\mathrm{3}}}=\mathrm{1}+\mathrm{4}\sqrt{{x}}+\mathrm{4}{x}=\mathrm{1}+\mathrm{2}^{\mathrm{2}} \sqrt{{x}}+\mathrm{4}{x} \\ $$$$\sqrt{\mathrm{16}{x}+....\sqrt{\mathrm{4}^{\mathrm{2009}} {x}+\mathrm{3}}}=\mathrm{1}+\mathrm{4}\sqrt{{x}}. \\ $$$$..{try}\:{to}\:{find}\:{last}\:{relation}\:{using}\:\mathrm{2}^{{n}} ,\mathrm{4}^{{m}} \\ $$
Commented by ruwedkabeh last updated on 11/Jan/21
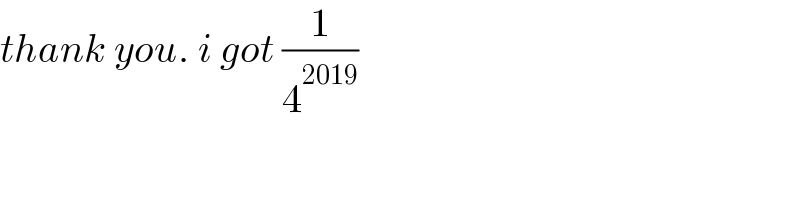
$${thank}\:{you}.\:{i}\:{got}\:\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2019}} } \\ $$
