
Question Number 128731 by TITA last updated on 09/Jan/21
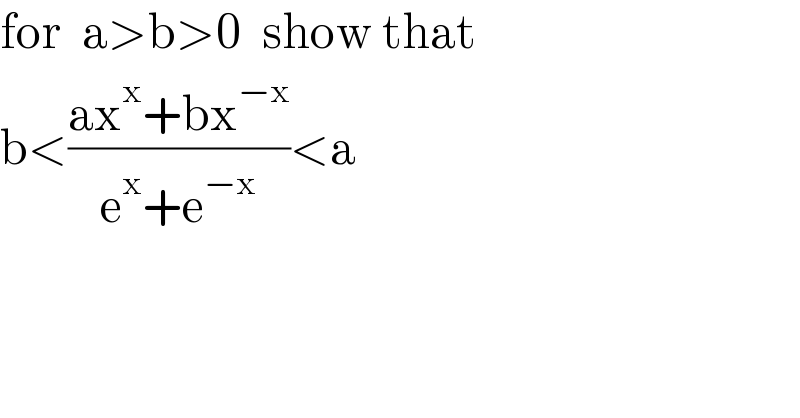
$$\mathrm{for}\:\:\mathrm{a}>\mathrm{b}>\mathrm{0}\:\:\mathrm{show}\:\mathrm{that} \\ $$ $$\mathrm{b}<\frac{\mathrm{ax}^{\mathrm{x}} +\mathrm{bx}^{−\mathrm{x}} }{\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} }<\mathrm{a} \\ $$
Commented byTITA last updated on 09/Jan/21

$$\mathrm{please}\:\mathrm{help} \\ $$
Commented byMJS_new last updated on 09/Jan/21

$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{true}\:\mathrm{if}\:\mathrm{we}\:\mathrm{are}\:\mathrm{free}\:\mathrm{to}\:\mathrm{choose}\:{x}\in\mathbb{R}^{+} \\ $$ $$\mathrm{i}.\mathrm{e}. \\ $$ $${b}=\mathrm{1}\wedge{a}=\mathrm{2} \\ $$ $$\mathrm{1}<\frac{\mathrm{2}{x}^{{x}} +{x}^{−{x}} }{\mathrm{e}^{{x}} +\mathrm{e}^{−{x}} }<\mathrm{2}\:\Leftrightarrow\:\mathrm{0}<{x}<\approx.\mathrm{937325}\vee\approx\mathrm{1}.\mathrm{83623}<{x}<\approx\mathrm{2}.\mathrm{72045} \\ $$ $$\mathrm{not}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:\mathrm{other}\:\mathrm{values}\:\mathrm{of}\:{x} \\ $$
