
Question Number 128712 by Study last updated on 09/Jan/21
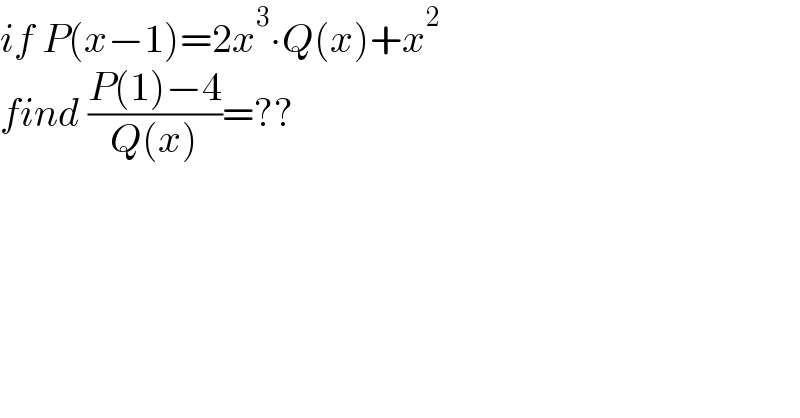
$${if}\:{P}\left({x}−\mathrm{1}\right)=\mathrm{2}{x}^{\mathrm{3}} \centerdot{Q}\left({x}\right)+{x}^{\mathrm{2}} \\ $$$${find}\:\frac{{P}\left(\mathrm{1}\right)−\mathrm{4}}{{Q}\left({x}\right)}=?? \\ $$
Commented by Adel last updated on 13/Jan/21
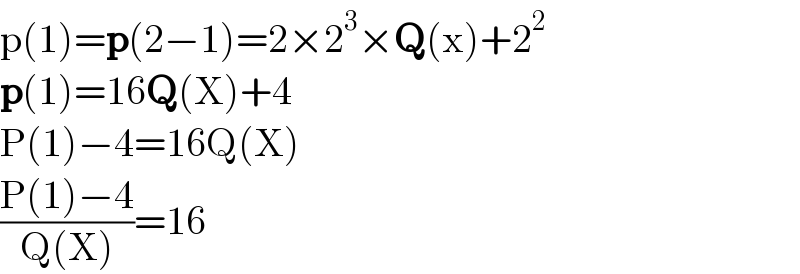
$$\mathrm{p}\left(\mathrm{1}\right)=\boldsymbol{\mathrm{p}}\left(\mathrm{2}−\mathrm{1}\right)=\mathrm{2}×\mathrm{2}^{\mathrm{3}} ×\boldsymbol{\mathrm{Q}}\left(\mathrm{x}\right)+\mathrm{2}^{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{p}}\left(\mathrm{1}\right)=\mathrm{16}\boldsymbol{\mathrm{Q}}\left(\mathrm{X}\right)+\mathrm{4} \\ $$$$\mathrm{P}\left(\mathrm{1}\right)−\mathrm{4}=\mathrm{16Q}\left(\mathrm{X}\right) \\ $$$$\frac{\mathrm{P}\left(\mathrm{1}\right)−\mathrm{4}}{\mathrm{Q}\left(\mathrm{X}\right)}=\mathrm{16} \\ $$
Answered by essafty last updated on 09/Jan/21

$$\mathrm{16} \\ $$$$ \\ $$
Commented by Study last updated on 09/Jan/21
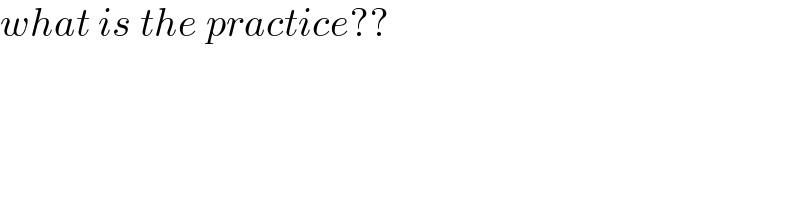
$${what}\:{is}\:{the}\:{practice}?? \\ $$
Answered by hknkrc46 last updated on 09/Jan/21
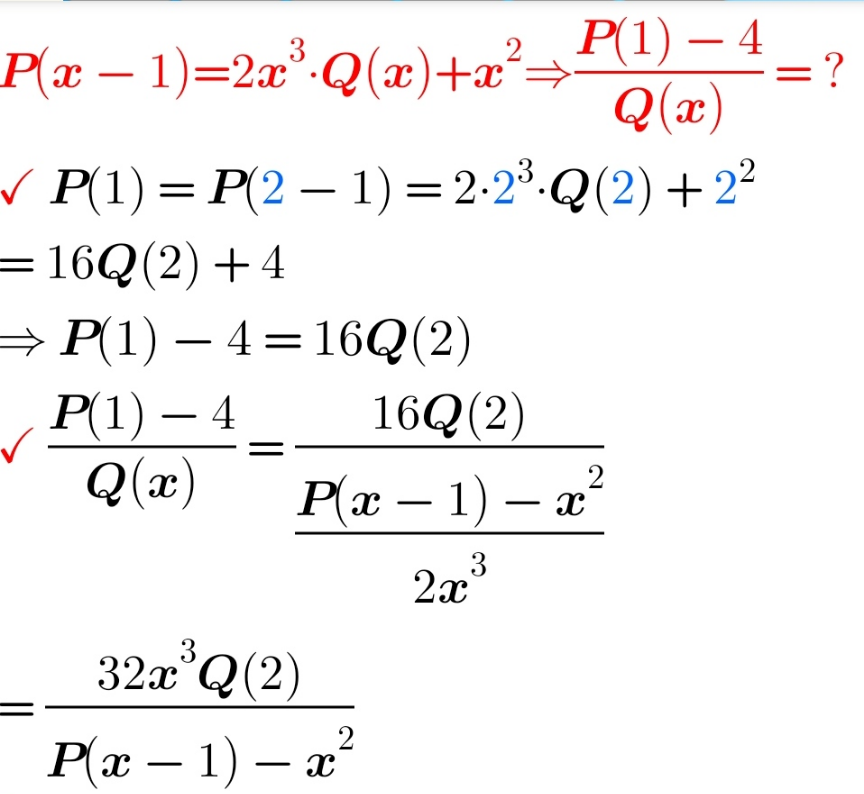
Commented by Study last updated on 10/Jan/21
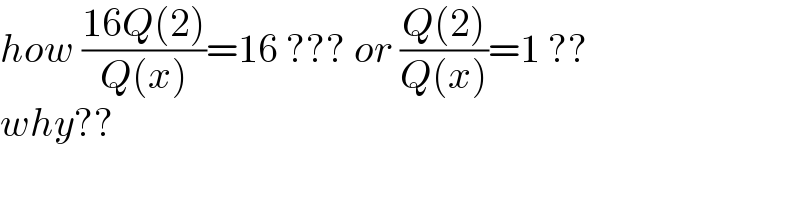
$${how}\:\frac{\mathrm{16}{Q}\left(\mathrm{2}\right)}{{Q}\left({x}\right)}=\mathrm{16}\:???\:{or}\:\frac{{Q}\left(\mathrm{2}\right)}{{Q}\left({x}\right)}=\mathrm{1}\:??\: \\ $$$${why}?? \\ $$
Commented by Study last updated on 11/Jan/21

$${why}?? \\ $$
Commented by Study last updated on 11/Jan/21

$${plz}\:{ans}\:{me} \\ $$
