
Previous in Differential Equation Next in Differential Equation
Question Number 128689 by bemath last updated on 09/Jan/21
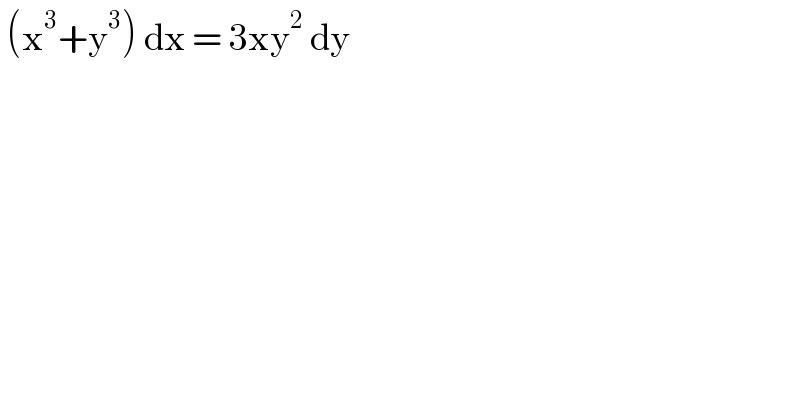
$$\:\left(\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} \right)\:\mathrm{dx}\:=\:\mathrm{3xy}^{\mathrm{2}} \:\mathrm{dy}\: \\ $$
Answered by liberty last updated on 09/Jan/21
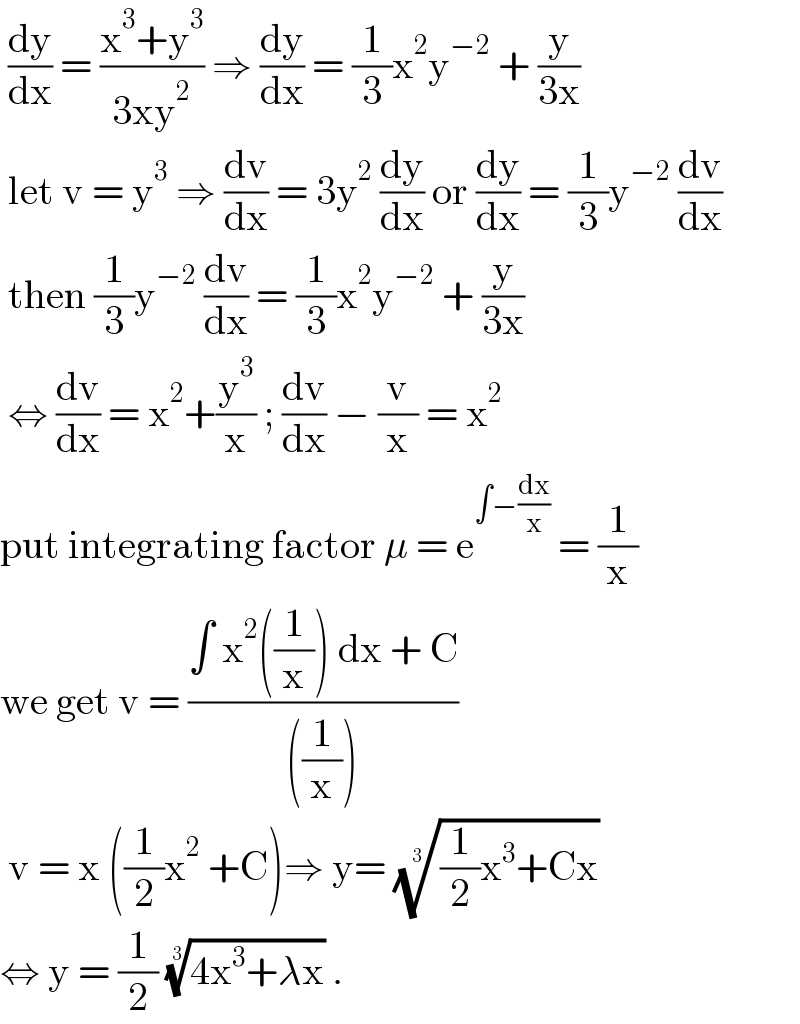
$$\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} }{\mathrm{3xy}^{\mathrm{2}} }\:\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} \mathrm{y}^{−\mathrm{2}} \:+\:\frac{\mathrm{y}}{\mathrm{3x}} \\ $$$$\:\mathrm{let}\:\mathrm{v}\:=\:\mathrm{y}^{\mathrm{3}} \:\Rightarrow\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\mathrm{3y}^{\mathrm{2}} \:\frac{\mathrm{dy}}{\mathrm{dx}}\:\mathrm{or}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{y}^{−\mathrm{2}} \:\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\:\mathrm{then}\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{y}^{−\mathrm{2}} \:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} \mathrm{y}^{−\mathrm{2}} \:+\:\frac{\mathrm{y}}{\mathrm{3x}} \\ $$$$\:\Leftrightarrow\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{x}}\:;\:\frac{\mathrm{dv}}{\mathrm{dx}}\:−\:\frac{\mathrm{v}}{\mathrm{x}}\:=\:\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{put}\:\mathrm{integrating}\:\mathrm{factor}\:\mu\:=\:\mathrm{e}^{\int−\frac{\mathrm{dx}}{\mathrm{x}}} \:=\:\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{v}\:=\:\frac{\int\:\mathrm{x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\mathrm{dx}\:+\:\mathrm{C}}{\left(\frac{\mathrm{1}}{\mathrm{x}}\right)} \\ $$$$\:\mathrm{v}\:=\:\mathrm{x}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \:+\mathrm{C}\right)\Rightarrow\:\mathrm{y}=\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{3}} +\mathrm{Cx}} \\ $$$$\Leftrightarrow\:\mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\sqrt[{\mathrm{3}}]{\mathrm{4x}^{\mathrm{3}} +\lambda\mathrm{x}}\:.\: \\ $$
