
Question Number 128641 by john_santu last updated on 09/Jan/21
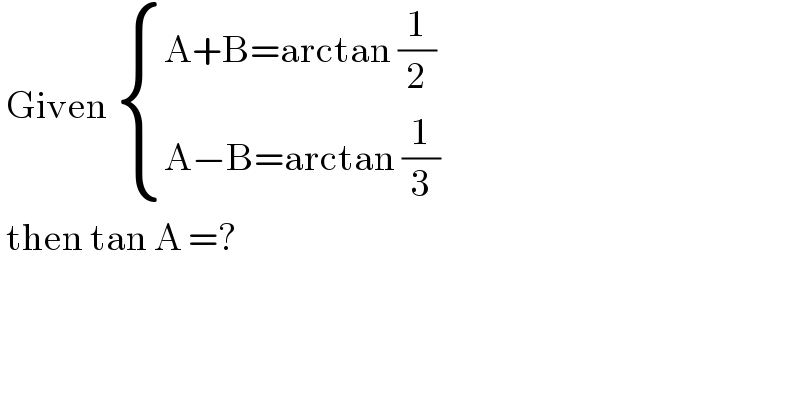
$$\:\mathrm{Given}\:\begin{cases}{\mathrm{A}+\mathrm{B}=\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{2}}}\\{\mathrm{A}−\mathrm{B}=\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}}\end{cases} \\ $$$$\:\mathrm{then}\:\mathrm{tan}\:\mathrm{A}\:=? \\ $$
Answered by liberty last updated on 09/Jan/21
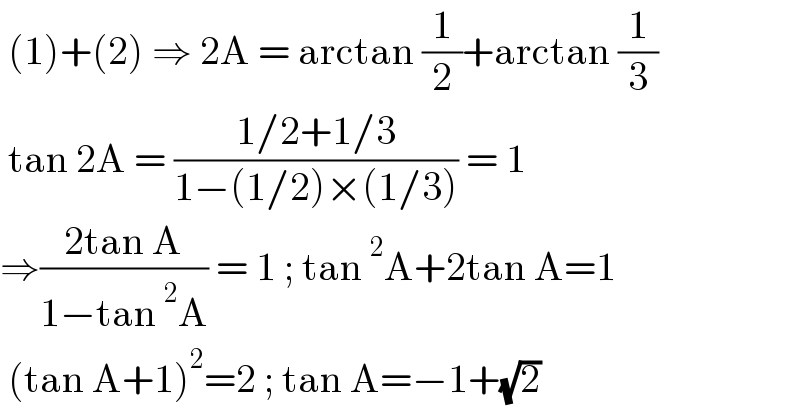
$$\:\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\:\Rightarrow\:\mathrm{2A}\:=\:\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\mathrm{tan}\:\mathrm{2A}\:=\:\frac{\mathrm{1}/\mathrm{2}+\mathrm{1}/\mathrm{3}}{\mathrm{1}−\left(\mathrm{1}/\mathrm{2}\right)×\left(\mathrm{1}/\mathrm{3}\right)}\:=\:\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{2tan}\:\mathrm{A}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{A}}\:=\:\mathrm{1}\:;\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{A}+\mathrm{2tan}\:\mathrm{A}=\mathrm{1} \\ $$$$\:\left(\mathrm{tan}\:\mathrm{A}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}\:;\:\mathrm{tan}\:\mathrm{A}=−\mathrm{1}+\sqrt{\mathrm{2}}\: \\ $$
